Решите систему всеми методами (крамер, метод обратной матрицы и так далее

Решите систему всеми методами (крамер, метод обратной матрицы и так далее
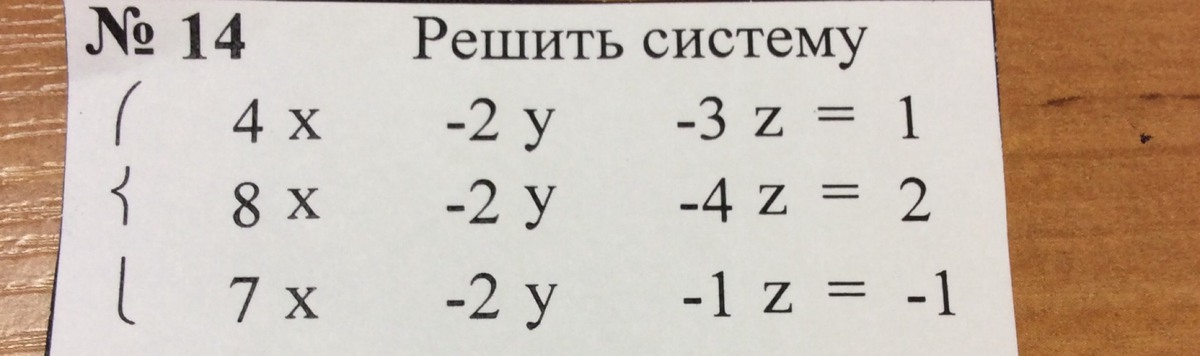
- Предмет:
  Математика
- Автор:
  elainayefx
- 5 лет назад

Ответы 3

не много не понял про обратную матрицу
- Автор:
  mario52
- 5 лет назад
- 0
что именно?
- Автор:
  mcmillan
- 5 лет назад
- 0
Крамера:Вычисляем главный определитель системы, вычислять определитель будем методом треугольников: $detA=\left|\begin{array}{ccc}4&-2&-3\\8&-2&-4\\7&-2&-1\end{array}ight|=\\=4*(-2)*(-1)+(-2)*7*(-4)+8*(-3)*(-2)-\\-((-3)*(-2)*7+(-2)*(-1)*8+4*(-2)*(-4))=\\=8+56+48-42-16-32=22$ Главный определитель системы не равен нулю, значит она имеет единственное решение.Заменим 1 столбец на столбец из констант и вычислим определитель, то же проделаем и со вторым и с 3 столбцом: $detA_x= \left|\begin{array}{ccc}1&-2&-3\\2&-2&-4\\-1&-2&-1\end{array}ight |=2-8+12+6-8-4=0$ $detA_y=\left|\begin{array}{ccc}4&1&-3\\8&2&-4\\7&-1&-1\end{array}ight|=-8-28+24+42-16+8=22$ $detA_z=\left|\begin{array}{ccc}4&-2&1\\8&-2&2\\7&-2&-1\end{array}ight|=8-28-16+14+16-16=-22$ Находим х, y, z: $x=\frac{|A_x|}{|A|}=\frac{0}{22}=0\\y=\frac{|A_y|}{|A|}=\frac{22}{22}=1\\z=\frac{|A_z|}{|A|}=\frac{-22}{22}=-1$ Метод обратной матрицы:Матрица А: $A=\left(\begin{array}{ccc}4&-2&-3\\8&-2&-4\\7&-2&-1\end{array}ight)$ Столбец неизвестных X: $X=\left(\begin{array}{ccc}x\\y\\z\end{array}ight)$ Столбец констант: $b=\left(\begin{array}{ccc}1\\2\\-1\end{array}ight)$ Обратную матрицу находим по формуле: $A^{-1}=\frac{1}{|A|}*A^T_m$ Где $A^T_m$ - транспонированная матрица алгебраических дополнений.Находим определитель матрицы А: $detA=\left|\begin{array}{ccc}4&-2&-3\\8&-2&-4\\7&-2&-1\end{array}ight|=22$ Находим $A^T_m$ . Для этого находим все миноры 2-ого порядка: $A_{11}=(-1)^{1+1}* \left|\begin{array}{ccc}-2&-4\\-2&-1\end{array}ight|=2-8=-6\\A_{12}=(-1)^{1+2}*\left|\begin{array}{ccc}8&-4\\7&-1\end{array}ight|=-(-8+28)=-20\\A_{13}=(-1)^{1+3}*\left|\begin{array}{ccc}8&-2\\7&-2\end{array}ight| =-16+14=-2\\A_{21}=(-1)^{2+1}*\left|\begin{array}{ccc}-2&-3\\-2&-1\end{array}ight|=-(2-6)=4\\A_{22}=(-1)^{2+2}*\left|\begin{array}{ccc}4&-3\\7&-1\end{array}ight|=-4+21=17\\A_{23}=(-1)^{2+3}*\left|\begin{array}{ccc}4&-2\\7&-2\end{array}ight|=-(-8+14)=-6$ $A_{31}=(-1)^{3+1}*\left|\begin{array}{ccc}-2&-3\\-2&-4\end{array}ight|=8-6=2\\A_{32}=(-1)^{3+2}*\left|\begin{array}{ccc}4&-3\\8&-4\end{array}ight|=-(-16+24)=-8\\A_{33}=(-1)^{3+3}*\left|\begin{array}{ccc}4&-2\\8&-2\end{array}ight|=-8+16=8$ $A_m^T= \left(\begin{array}{ccc}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{array}ight)^T= \left(\begin{array}{ccc}-6&-20&-2\\4&17&-6\\2&-8&8\end{array}ight)^T=\\= \left(\begin{array}{ccc}-6&4&2\\-20&17&-8\\2&-8&8\end{array}ight)$ Находим $A^{-1}$ : $A^{-1}=\frac{1}{|A|}*A^T_m=\frac{1}{22}*\left(\begin{array}{ccc}-6&4&2\\-20&17&-8\\2&-8&8\end{array}ight)$ $X= \left(\begin{array}{ccc}x\\y\\z\end{array}ight) =A^{-1}b=\frac{1}{22}*\left(\begin{array}{ccc}-6&4&2\\-20&17&-8\\2&-8&8\end{array}ight)* \left(\begin{array}{ccc}1\\2\\-1\end{array}ight)=\\=\frac{1}{22}* \left(\begin{array}{ccc}-6*1+4*2+2*(-1)\\-20*1+17*2+(-8)*(-1)\\2*1+(-8)*2+8*(-1)\end{array}ight)=\frac{1}{22}* \left(\begin{array}{ccc}0\\22\\-22\end{array}ight)= \left(\begin{array}{ccc}0\\1\\-1\end{array}ight)$ Метод Гаусса:Записываем расширенную матрицу (A|b) и приводим матрицу A к верхнему треугольному виду путём элементарных преобразований.1) Отнимаем от 2 строки 3-ю, после меняем 1 и 2 строки. $\left(\begin{array}{ccc}4&-2&-3\\8&-2&-4\\7&-2&-1\end{array}ight| \left\begin{array}{ccc}1\\2\\-1\end{array}ight)= \left(\begin{array}{ccc}4&-2&-3\\1&0&-3\\7&-2&-1\end{array}ight| \left\begin{array}{ccc}1\\3\\-1\end{array}ight)=\\= \left(\begin{array}{ccc}1&0&-3\\4&-2&-3\\7&-2&-1\end{array}ight| \left\begin{array}{ccc}3\\1\\-1\end{array}ight)$ 2) Отнимаем от второй первую строку умноженную на 4, после от 3-ей первую строку умноженную на 7. $\left(\begin{array}{ccc}1&0&-3\\4&-2&-3\\7&-2&-1\end{array}ight| \left\begin{array}{ccc}3\\1\\-1\end{array}ight)=\left(\begin{array}{ccc}1&0&-3\\0&-2&9\\0&-2&20\end{array}ight| \left\begin{array}{ccc}3\\-11\\-22\end{array}ight)$ 3) от 3-ей отнимаем вторую. $\left(\begin{array}{ccc}1&0&-3\\0&-2&9\\0&-2&20\end{array}ight| \left\begin{array}{ccc}3\\-11\\-22\end{array}ight)=\left(\begin{array}{ccc}1&0&-3\\0&-2&9\\0&0&11\end{array}ight| \left\begin{array}{ccc}3\\-11\\-11\end{array}ight)$ Дальше применяем обратный ход. То есть мы получили такую систему(эквивалентную нашей изначальной):{1·x+0·y-3·z=3{ -2·y+9·z=-11{ 11z=-11 $z=\frac{-11}{11}=-1$ $-2y+9*(-1)=-11\\-2y=-2\\y=1$ $x+0-3*(-1)=3\\x=0$ Есть ещё метод Гаусса-Жордана, мы как и в методе Гаусса строим расширенную матрицу,а потом уже приводим A к единичному виду. После этого столбец b и будет решением. Это одна из разновидностей метода Гаусса, поэтому я не буду её писать)
- Автор:
  cheyenne84
- 5 лет назад
- 0
Добавить свой ответ