Задать вопрос Регистрация
Помочь другим

  • помогите упростить выражение...и найти его значение

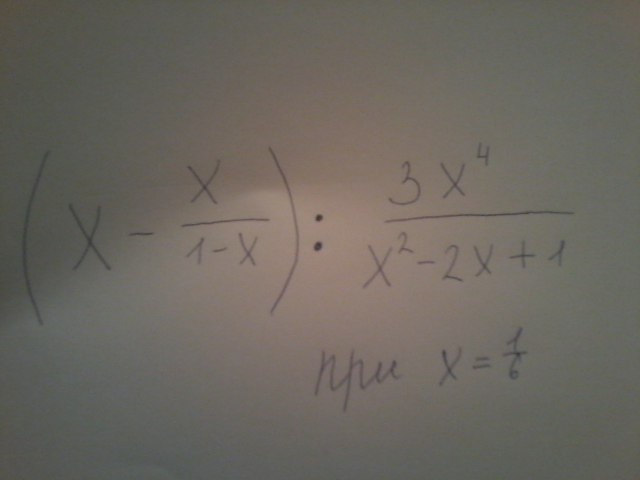
    question img

Ответы 2

  • (x+ \frac{x}{x-1} ): \frac{3 x^{4} }{ (x-1)^{2} } = \frac{x(x-1)+x}{x-1}* \frac{ (x-1)^{2} }{3 x^{4} } = \frac{ x^{2}-x+x }{x-1} * \frac{ (x-1)^{2} }{3 x^{4} }= \frac{ x^{2} *(x-1)}{3 x^{4} } = \frac{x-1}{3 x^{2} } \frac{ \frac{1}{6}-1 }{3* (\frac{1}{6}) ^{2} } = \frac{ -\frac{5}{6} }{ \frac{1}{12} } =- \frac{5*12}{6} =-10

  • Сначала свернем знаменатель второй дроби:x^2-2*x+1=0 D=4-4=0 x=2/2=1 Тогда x^2-2*x+1=(x-1)*(x-1)

    Теперь все исходное выражение:

     (х*(1-х)-х) / (1-х) * (х-1)^2/(3*x^4) = -(-x^2)/(x-1) * (x-1)^2/(3*x^4)=(x-1)/(3*x^2)

    При х=1/6 получим (1/6-1)/(3*1/36)=(-5/6) / (1/12)=(-5/6)*(12/1)=-5*2=-10

    • Автор:

      taye
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years