-
Решите уравнения:
1. lim x->0 (e^-x-e^x)/sin3x)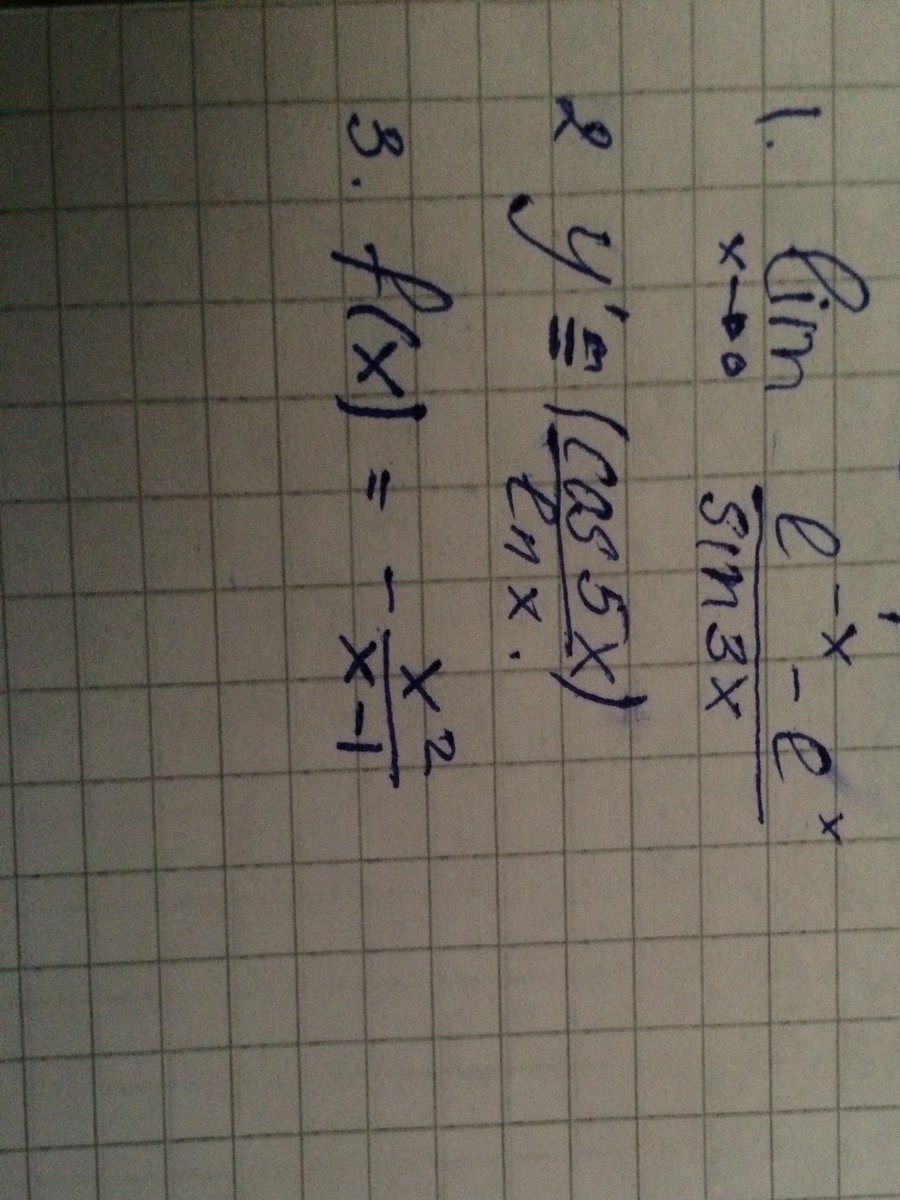
-
Предмет:
Математика -
Автор:
sergio58 - 5 лет назад
-
Ответы 1
-

-
Автор:
jeffersonyevm - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Ещё вопрос по РПС... Даю 15 баллов
Решить задачу-головоломку:
На сковороде помещается 2 кусочка хлеба. На поджаривание кусочка с одной стороны требуется одна минута. Как поджарить 3 кусочка хлеба за 3 минуты с обеих сторон?-
Предмет:
Другие предметы -
Автор:
ferrell - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Какие нерешённые глобальные проблемы вам известны? Перечислите все.Почему их называют глобальными?
-
Предмет:
Обществознание -
Автор:
amparo - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
делимое 32 делитель 8 найти частное
-
Предмет:
Математика -
Автор:
angiegraves - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Спасибо вам большое, может и с этим сможете помочь:з
Пожалуйста-
Предмет:
Английский язык -
Автор:
sutton - 5 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
