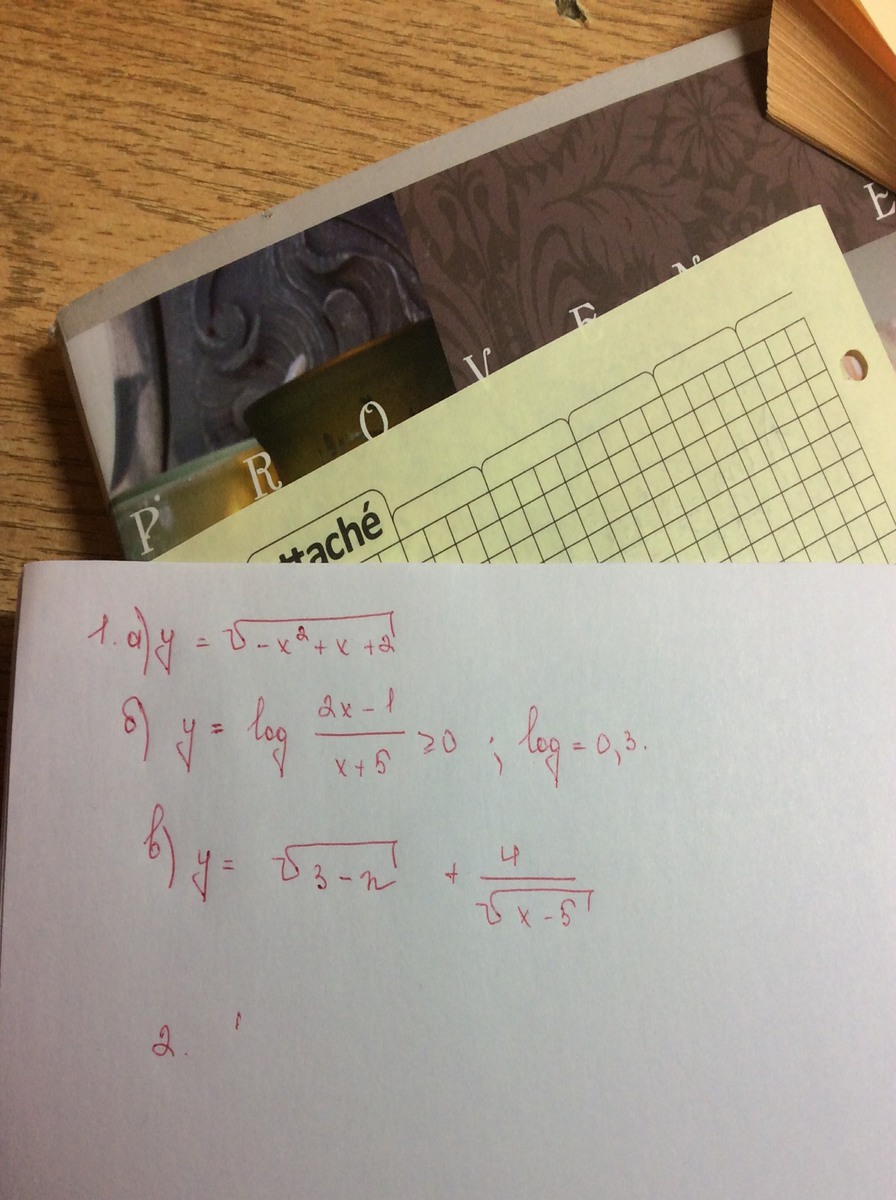
Помогите пожалуйста))найти область определения функции, спасибо заранее))

через полчаса, ОК?

да, хорошо))

Я не совсем понял в б) - что там за log = 0,3?

я не так записала, там log 0,3 2x-1/ x+5

Ну, это ничего не меняет...)))

y = √-x²+x+2ООФ:  -x²+x+2≥0         D=b²-4ac=1+8=9         x₁=(-b+√D)/2a=(-1+3)/(-2)=-1         x₂=(-b-√D)/2a=(-1-3)/(-2)=2-x²+x+2= -(x+1)(x-2)Решаем 2 системы неравенств:  x+1≥0            x+1≤0                                                       x-2≤0             x-2≥0                           получаем:       х ≥ -1             х ≤ -1                                                     х≤ 2              х ≥ 2Правая система решения не имеет.Левая система имеет решение:  x∈[-1; 2]Это решение и будет являться областью определения данной функцииПродолжаем...)))y = log (2x-1)/(x +5)ООФ: (2x-1)/(x +5)>0  и  x≠ -5Решаем 2 системы неравенств:   2x - 1 > 0               2x - 1 < 0                                                       x + 5 > 0               x + 5 < 0                              получаем:          x > 1/2                  x < 1/2                                                     x > -5                    x < -5Решением каждой системы неравенств будет пересечение решений каждого:                                          x∈ (1/2; ∞)П(-5; ∞)          x∈ (-∞; 1/2)П(-∞; -5)                                                 x∈ (1/2; ∞)                     x∈ (-∞; -5)Общим решением будет объединение решений каждой системы:                                                      x∈ (-∞; -5)U(1/2; ∞)Таким образом, область определения функции:x∈ (-∞; -5)U(1/2; ∞) Ну и третье.y = √3-x + 4/(√x-5)ООФ: 3 - x ≥ 0  и  x - 5 > 0Тогда:   х ≤ 3    и   х > 5    Ни одно из значений х не удовлетворяет ООФ => функция решений не имеет.Или так: решением функции будет пустое множество (кружочек такой перечеркнутый..)))                    Вот, как-то так..)))