-
ПОМОГИТЕ ПОЖАЛУЙСТА, У МЕНЯ С ОТВЕТОМ НЕ СОВПАДАЕТ, БЛИН УЖЕ КОТОРЫЙ РАЗ ПИШУ НИКТО НЕ ОТВЕЧАЕТ И НЕ ПОМОГАЕТ ((9 (9 (0
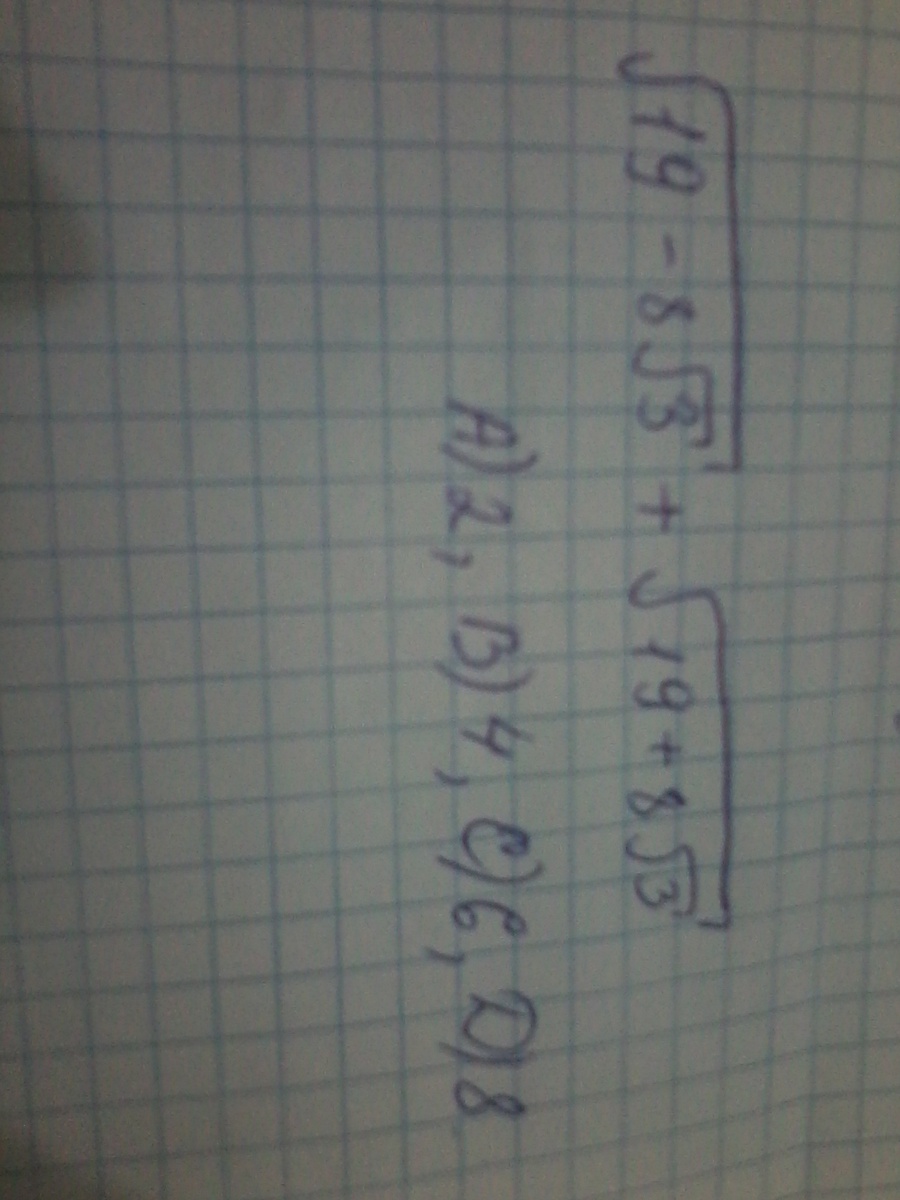
-
Предмет:
Математика -
Автор:
darwinaep4 - 6 лет назад
-
Ответы 6
-
у меня 3 получается (((0(
-
Автор:
karlaudku - 6 лет назад
-
0
-
-
дополним решением
-
Автор:
shirleyni7j - 6 лет назад
-
0
-
-
спасибо за объяснение)
-
Автор:
victoriaxtuw - 6 лет назад
-
0
-
-
спасибо))
-
Автор:
ceciliamay - 6 лет назад
-
0
-
-
правильный ответ 8Нужно все в квадрат возвестиА потом корень от получившегося взять.Возводим все в квадратполучается квадрат первого числа + удвоенное произведение + квадрат второго.19-8√3 + 19 + 8√3 + 2*√((19-8√3)(19+8√3))слева получается 38, а под корнем сворачиваем разность квадратов.38+2*√19^2 -(8√3)^2 = 38 + 2*√(361-64*3) = 38 + 2*√(361-192) = 38 + 2*√(169) = 38+2*13 = 38+26 = 64Так как мы сначала возводили в квадрат - теперь от результата берем кореньПолучается √64 = 8
-
Автор:
skinny jeansgbgs - 6 лет назад
-
0
-
-
Для того, чтобы решить выражение подобного типа необходимо выделить полный квадрат в обоих подкоренных выражениях.Рассмотрим первое подкоренное выражение:
Нам нужно подобрать такое число, чтобы его удвоенное произведение давало -8 корней из 3.То есть в произведении двух чисел (a и b) должно получаться 4 корня из 3,а в сумме квадратов этих двух чисел должно быть 19:
Данный пример не отличается огромными значениями так что можно заметить, что произведение 4 и корня из 3 и является нашим полным квадратом:
Для второй скобки полный квадрат будет аналогичен, лишь знак между числами будет отличаться. Таким образом мы имеем:
Избавимся от корня:
Теперь необходимо избавиться от модуля. Проанализируем значение первого модуля: он однозначно положительный.Второй модуль также является положительным, так как 4 больше чем корень из 3 (корень из 16 больше корня из 3)Таким образом, мы можем попросту отбросить модуль.Корень из трех взаимоуничтожится. Останется 4+4=8Ответ: 8
-
Автор:
evans - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- какой необыкновенной особенностью обладают физика
-
помогите решить уровнения !!! Срочно!!! 2x+4x=30;7y+y-2y=24;
-
Предмет:
Математика -
Автор:
akira14 - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Say a noun.Your partner gives a definition using a relative pronoun/adverb.
-
Предмет:
Английский язык -
Автор:
dot - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Нужно краткое сообщение о армии РФ
-
Предмет:
Обществознание -
Автор:
silly gilly - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
