Задать вопрос Регистрация
Помочь другим

  • Математика вычислить, какие пары плоскостей являются параллельными, а какие - перпендикулярными.

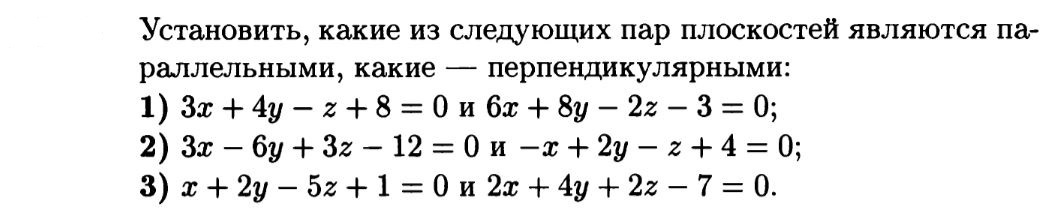
    question img

Ответы 3

  • А как мы получили коэффициент 1/2 под буквой а)

    • Автор:

      lillys64m
    • 5 лет назад
    • 0
  • Так визуально видно... поделите первые координаты друг на друга... для первой плоскости A=3 для второй A=6... вот и коэффициент...

    • Автор:

      thomas99
    • 5 лет назад
    • 0
  • Для плоскости, заданной уравнениемAx+By+Cz+D=0вектор с координатами\vec n = (A;B;C)является вектором нормали (перпендикулярен к плоскости)Таким образом, если для двух плоскостей нормальные вектора коллинеарны - то плоскости - параллельны, а если перпендикулярны - то перпендикулярны и плоскости.Проверим для наших примеров.a)(3;4;-1) = \frac{1}{2}*(6;8;-2)Вектора коллинеарны -> плоскости - параллельныb)(3;-6;3) = -3*(-1;2;-1)Вектора коллинеарны -> плоскости - параллельныБолее того, для параметра D также верно-12 = -3*4т.е. плоскости не просто параллельны, но и совпадаютc)(1;2;-5) = \frac{1}{2}*(2;4;-10)e\frac{1}{2}*(2;4;2)Вектора не коллинеарны -> плоскости - не параллельны.Проверим ортогональность векторов(1;2;-5)*(2;4;2)=1*2+2*4-5*2=2+8-10=0Скалярное произведение векторов равно 0 -> вектора перпендикулярны -> плоскости перпендикулярны

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years