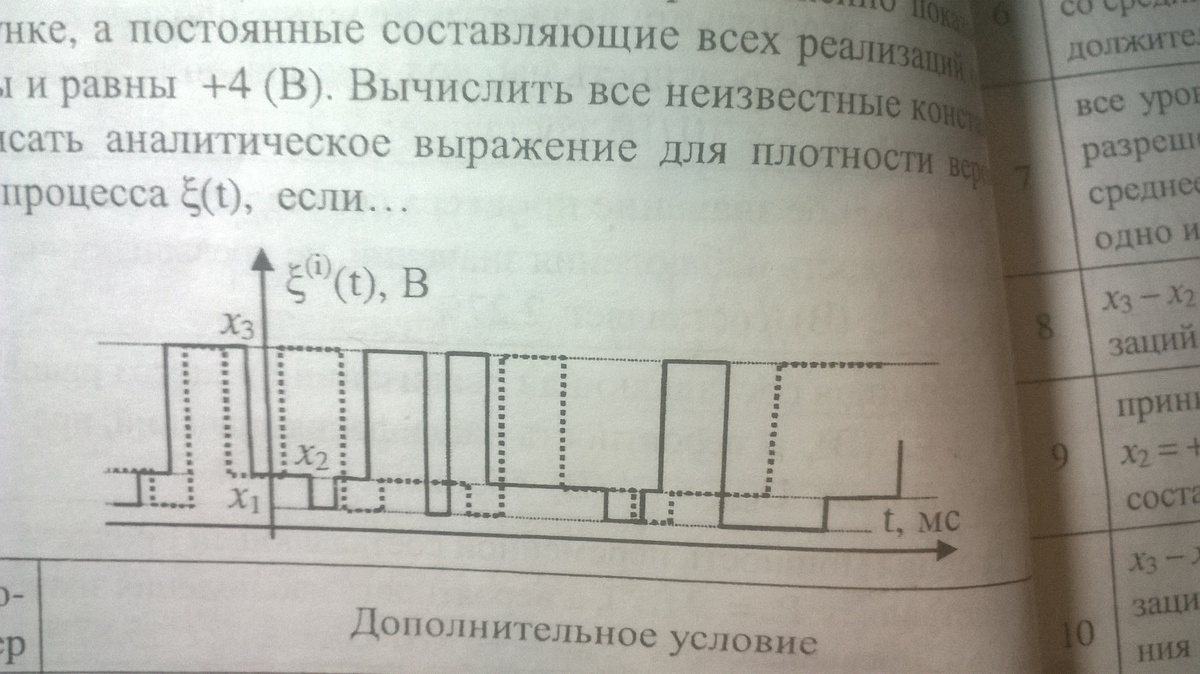
Эргодический случайный процесс в каждый момент времени принимает какое-то одно из трех разрешенных значений. Форма реализации этого процесса приближенно показана на рисунке, а постоянные составляющие всех реализаций одинаковы и равны +4 Вольта. Вычислить все неизвестные константы и записать аналитическое выражение для плотности вероятности процесса кси(t), если все уровни x1 x2 x3 больше нуля, каждый последующий разрешенный уровень вдвое больше предыдущего, а среднее время прибывания реализации на каждом уровне одно и то же.

так как среднее время прибывания реализации на каждом уровне одно и то же. то функция плотности вероятности имеет вид p = 1/3, если х = х1p = 1/3, если х = х2p = 1/3, если х = х3известно что x2=2*x1известно что x3=2*x2=4*x1Mx=1/3*x1+1/3*x2+1/3*x3=1/3*(x1+x2+x3)=1/3*(x1+2*x1+4*x1)=7*x1/3 = 4x1 = 3*4/7=12/7x2=24/7x3=48/7ответх - ДСВ p = 1/3, если х = 12/7p = 1/3, если х = 24/7p = 1/3, если х = 48/7p = 0, если х - другое число