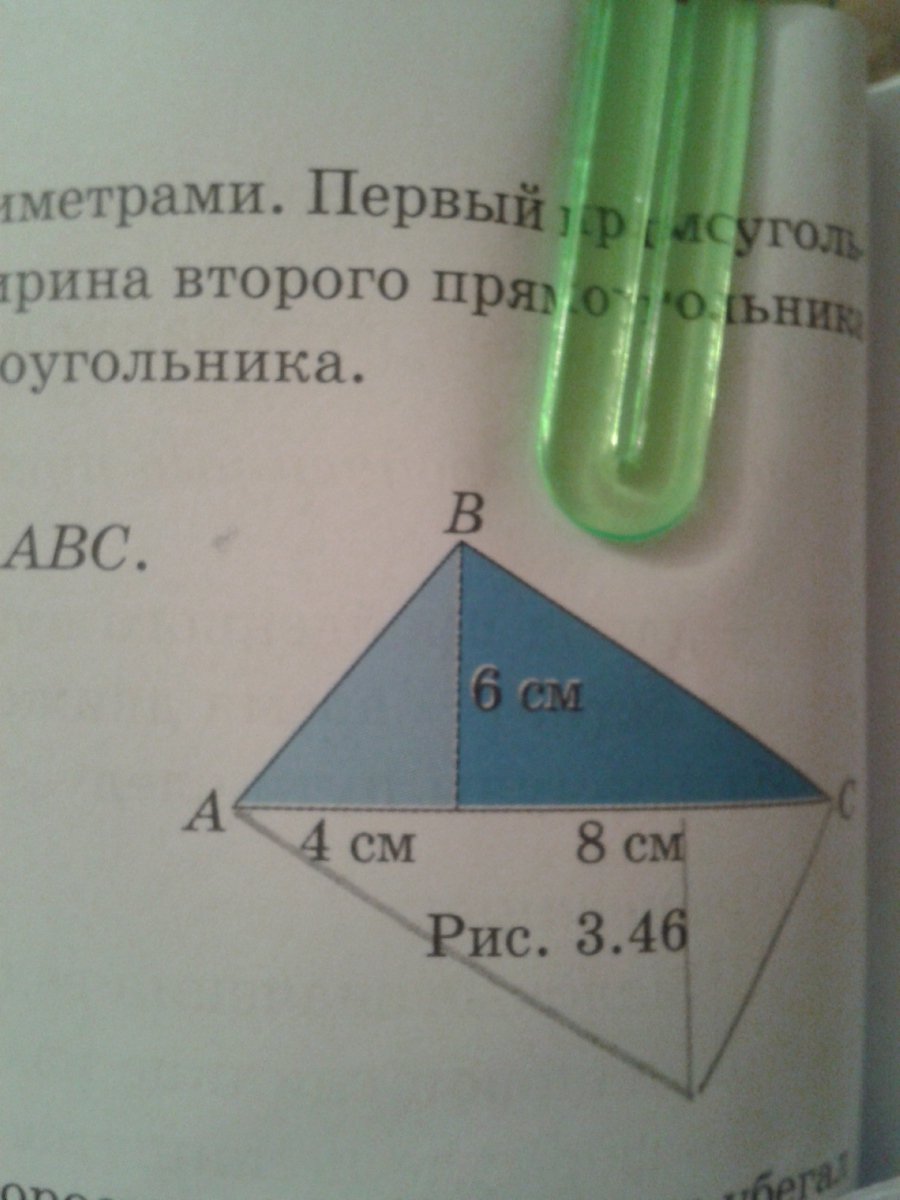
на рисунке изображен треугольник АВС дополните до прямоугольника,найдите площадь прямоугольника,найдите площадь треугольника АВС

Задача 1. Достроить ΔАВС до прямоугольника.

Свойство прямоугольников -  стороны попарно равны между собой и перпендикулярны.

Построение на рисунке в приложении. Высота треугольника BD перпендикулярна основанию АС. Сторона ЕF||AC, а стороны AE и CF параллельны высоте BD. Получили прямоугольник AEFC.

Здесь очень наглядно видно, что площадь треугольника АВС равна половине площади прямоугольника AEFC.

Площадь треугольника вычисляется по формуле:

S = 1/2*a*b, где: а - основание,  b -  высота треугольника.

Площадь прямоугольника по формуле: S = a*b -  в два раза больше площади треугольника.

Решение задачи на рисунке.

Дан треугольник ABC :   AC = 4 см + 8 см = 12 см;  BN⊥AC; BN = 6 см

Из точек А и С проведем перпендикуляры к стороне АС, равные высоте треугольника:

AF ⊥ AC   и   CM ⊥ AC;  AF = CM = BN = 6 см

Получился прямоугольник  AFMC. Площадь этого прямоугольника равна произведению сторон  S = AC · AF = 12·6 = 72 см².

Рассмотрим прямоугольник  AFBN.  Диагональ прямоугольника АВ делит его на два равных треугольника ΔAFB = ΔABN.

Рассмотрим прямоугольник  NBMC.  Диагональ прямоугольника ВC делит его на два равных треугольника ΔNBC = ΔBMC.

Площадь треугольника  АВС  состоит из площадей треугольников ABN  и  NBC,  которые в сумме составляют половину площади прямоугольника AFMC   ⇒

см²

Ответ: площадь прямоугольника  72 см²;

           площадь треугольника АВС  36 см²