-
Это логарифмические неравенства, если что :)
Решите, какие сможете, буду очень благодарен!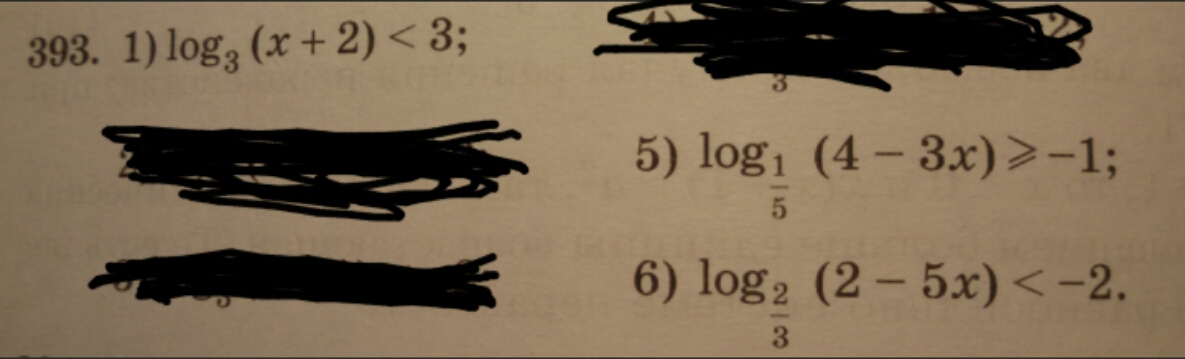
-
Предмет:
Математика -
Автор:
opie - 6 лет назад
-
Ответы 6
-
тут картинки нет
-
Автор:
blanchard - 6 лет назад
-
0
-
-
сама решила
-
Автор:
peteyud85 - 6 лет назад
-
0
-
-
2 погрузился
-
Автор:
seniorgkyw - 6 лет назад
-
0
-
-
но спасибо :)
-
Автор:
jethrocain - 6 лет назад
-
0
-
-
пожалуйста:)
-
Автор:
giovani - 6 лет назад
-
0
-
-
ОДЗ: х+2>0⇒x>-2
Ответ: -2<x<25 ** основание больше 1, значит знак сохраняется
ОДЗ: 4-3x>0 ⇒x<4/3
*** основание меньше 1, значит знак меняетсяОтвет: x⊂(-1/3,4/3)
ОДЗ: 2-5x>0 ⇒x>2/5
Ответ: x<-1/20
-
Автор:
fido - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Ответьте на тест
1. Определите, что предоставляет растительной клетке желтой окраски:
a) ксантофил б) хлорофилл в) каротин г) крахмальные зерна
2. Какая ткань НЕ относится к растительным тканям:
a) соединительная б) основная в) проводящая г) механическая
3. Какой орган относится к генеративным органам растений:
a) побег б) лист в) корень г) цветок
4. Определите, где образуются мужские половые клетки цветковых растений:
а) пыльники тычинок б) семенные зачатки в) пестик г) пыльцевое зерно
5. У взрослых сфагновых мхов отсутствуют:
а) листья б) ризоиды в) стебель г) хлорофилл
6. С помощью каких органелл движется лейшмания:
а) жгугитик б) реснички в) ундулирующая мембрана г) псевдоподии
7. Определите, из скольких слоев клеток состоит тело кишечнополостных:
а) из четырех б) из трех в) из двух г) из одного
8. Определите орган, при отсутствии которого кошачий сосальщик отличается от белой планарии:
а) выделительная система б) кишечник в) глаза г) нервный узел
9. Определите, чем можно заразиться, употребляя в пищу недостаточно мытые овощи:
а) бычий цепень б) кошачий сосальщик в) лентец широкий г) печеночный сосальщик
10. Какое животное относится к классу паукообразные:
а) мокрица б) клещ в) клоп г) креветка
-
Предмет:
Биология -
Автор:
nemoconway - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
придумайте стих с этими рифмами:дневник+ученик,ночи+сочи,тетрадь+кровать
-
Предмет:
Литература -
Автор:
williamson - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Как на письме оформляются предложения с прямой речью, которая стоит до и после стов автора? Покажи с помощью схем. Помогите решить, учитель сказал сделать 6 схем.
-
Предмет:
Русский язык -
Автор:
schnookumsnjkb - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
проверочное слово для слова белок
-
Предмет:
Русский язык -
Автор:
lincoln49 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
