Задать вопрос Регистрация
Помочь другим

  • Интересует решение 5го примера на фото. Желательно письменное решение. 

    И еще, правильные ли ответы у меня получились:

    1) х<1

    2) x<3

    3) x>1,5

    4) x >= 13? Проверьте, правильно ли. Спасибо заранее!

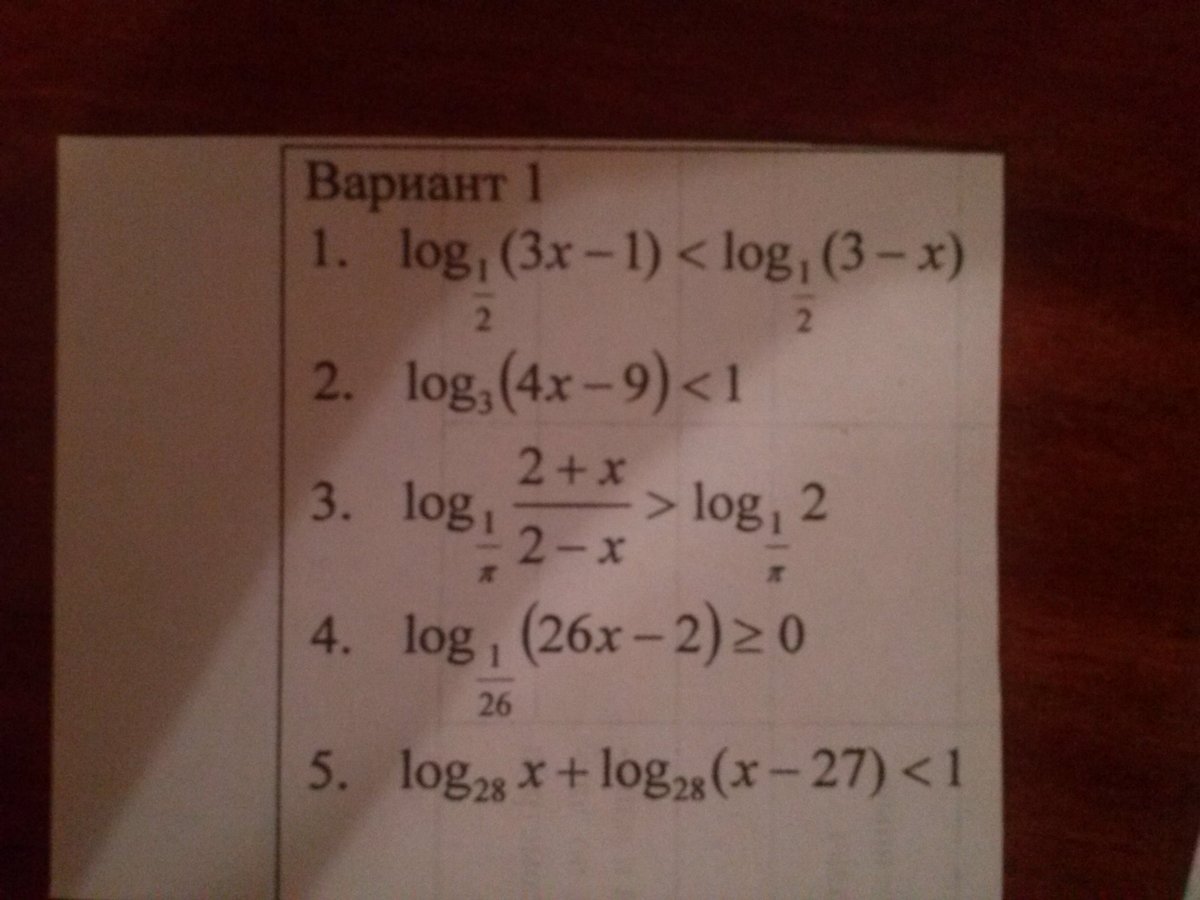
    question img

Ответы 1

  • 1) правильный ответ x>1

    2) верно

    3) правильный ответ x<1,5

    4) неверно:

    \log_{\frac1{26}}(26x-2)\leq0\\ 26x-2\geq\left(\frac1{26}ight)^0\\ 26x-2\geq1\\ 26x\geq3\\ x\geq\frac3{26}

    5) Сумма логарифмов = логарифму произведения:

    \log_{28}x+\log_{28}(x-27)<1\\ \log_{28}(x^2-27x)<1\\ x^2-27x<28\\ x^2-27x-28<0\\ x^2-27x-28=0\\ D=729+4\cdot28=841=29^2\\ x_1=-1,\;x_2=28\\ x=-2\Rightarrow x^2-27x-28=4+54-28=30>0\\ x=0\Rightarrow x^2-27x-28=0-0-28=-28<0\\ x=29\Rightarrow x^2-27x-28=841-783-28=30>0\\ x\in(-1;\;28)

     

    P.S. При решении логарифмических неравенств всегда проверяйте основание логарифма. Если оно <1, то знак неравнества меняется на противоположный, если >1 - знак остаётся.

    • Автор:

      tomcat
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years