-
Помогите пожалуйста решить на множестве R уравнения:
(пример в тетради и №1(а,б,в,д),№5(б,в)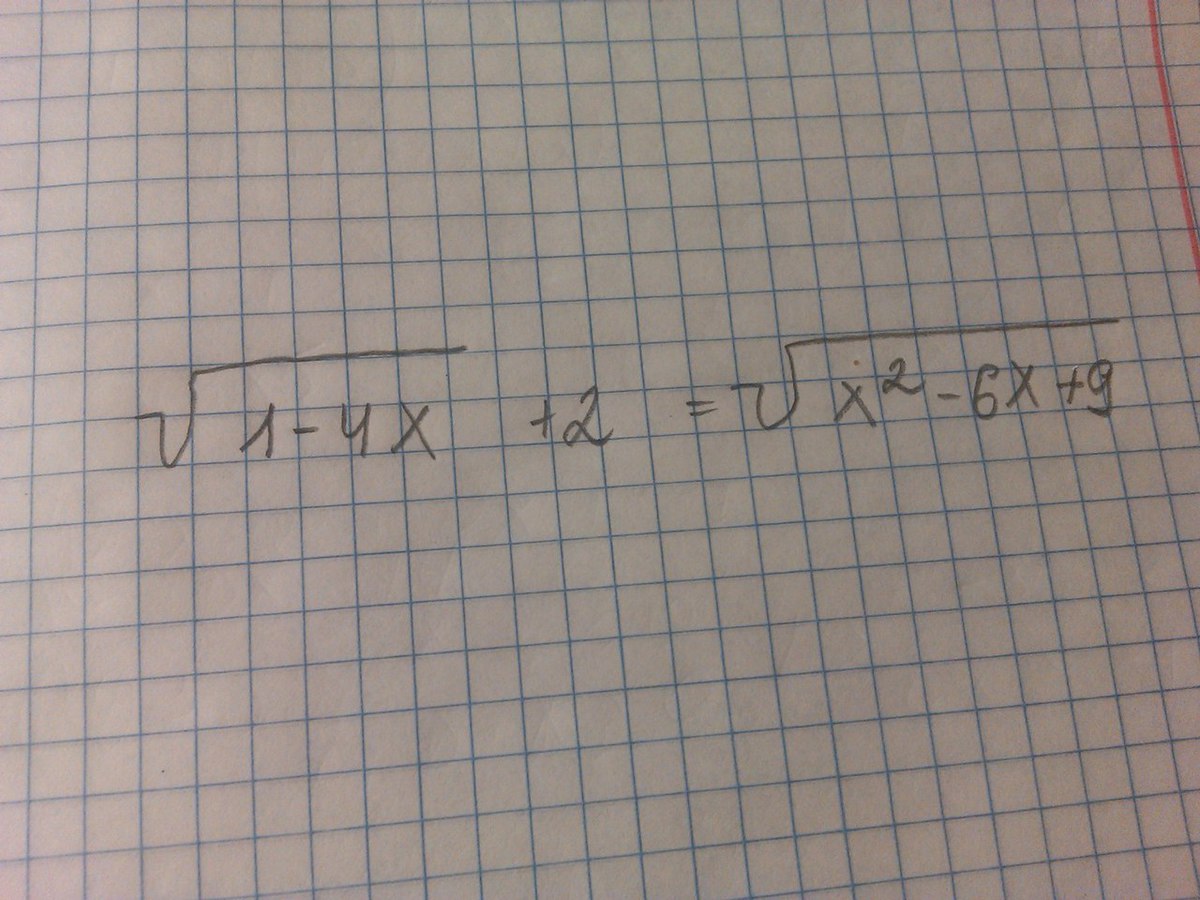

-
Предмет:
Математика -
Автор:
levi9 - 6 лет назад
-
Ответы 1
-
√(1 - 4x) + 2 = √(x^2 - 6x + 9)√(1 - 4x) + 2 = √(x - 3)^2 = |x - 3|Область определения 1 - 4x >= 0x <= 1/4 < 3При x < 3 будет |x - 3| = 3 - x√(1 - 4x) = 3 - x - 2 = 1 - xВозводим всё в квадрат1 - 4x = (1 - x)^2 = 1 - 2x + x^2x^2 + 2x = 0x1 = 0 - подходитx2 = -2 - подходит1) а) √(x + 1) = x - 5Область определения x >= -1Корень арифметический, то есть неотрицательный, поэтомуx - 5 >= 0; x >= 5Возводим всё в квадратx + 1 = (x - 5)^2 = x^2 - 10x + 25x^2 - 11x + 24 = 0(x - 3)(x - 8) = 0По области определения x >= 5, поэтому подходит толькоx = 8б) √(x - 1) = x - 7Корень арифметический, поэтому x >= 7Возводим всё в квадратx - 1 = (x - 7)^2 = x^2 - 14x + 49x^2 - 15x + 50 = 0(x - 5)(x - 10) = 0По области определения x >= 7 подходит только x = 10в) √(x + 1) = 2x + 1Корень арифметический, поэтому x >= -1/2Возводим всё в квадратx + 1 = (2x + 1)^2 = 4x^2 + 4x + 14x^2 + 5x = 0x1 = 0 - подходитx2 = -4/5 = -8/10 < -5/10 - не подходитx = 0д) √(17 + 2x - 3x^2) = x + 1Область определения-3x^2 + 2x + 17 >= 0D = 2^2 - 4(-3)*17 = 4 + 204 = 206x1 = (-2 - √206)/(-6) = (2 + √206)/6 ~ 2,72x2 = (-2 + √206)/(-6) = (2 - √206)/6 ~ -2,06Левая часть неотрицательна при x ∈ [x2; x1]Корень арифметический, поэтому x >= -1Область определения x ∈ [-1; (2 + √206)/6]Возводим всё в квадрат17 + 2x - 3x^2 = (x + 1)^2 = x^2 + 2x + 14x^2 - 16 = 4(x - 2)(x + 2) = 0Подходит только x = 25) б) √(x + 3) = x - 1Корень арифметический, поэтому x >= 1Возводим всё в квадратx + 3 = (x - 1)^2 = x^2 - 2x + 1x^2 - 3x - 2 = 0D = 3^2 - 4*(-2) = 9 + 8 = 17x1 = (3 - √17)/2 < 0 - не подходитx2 = (3 + √17)/2 > 1 - подходитв) √(5 - x) + √(x - 6) = xОбласть определения:{ 5 - x >= 0; x <= 5{ x - 6 >= 0; x >= 6Эта система решений не имеет, и само уравнение тоже.
-
Автор:
ignacioharper - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите решить задачу по условию Из 40 опрошенных 32 любят молоко,21-лимонад а 15-и молоко и лимонад.Сколько человек не любят лимонад
-
Предмет:
Математика -
Автор:
leohi3h - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
РЕБЯТА ПОМОГИТЕ СРОЧНООООООООООО
НАЙДИТЕ ЧИСЛО,КОТОРОГО РАВНО ЗНАЧЕНИЮ ВЫРАЖЕНИЮ
(4\7*5\3)-(4\7*4\3)
НАЙДИТЕ ЧИСЛО,93% КОТОРОГО РАВНО ПРОИЗВЕДЕНИЮ ЧИСЕЛ 3,5\12 И 2,2\41-
Предмет:
Математика -
Автор:
isidrol4bf - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Что такое перелив технологий? (технологический перелив)
-
Предмет:
Обществознание -
Автор:
milesandrade - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
схема питания в степной зоне
-
Предмет:
Окружающий мир -
Автор:
prettylqo3 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
