Задать вопрос Регистрация
Помочь другим

  • Иррациональное уравнение решите, пожалуйста!!! Используя замену t
    Заранее СПАСИБО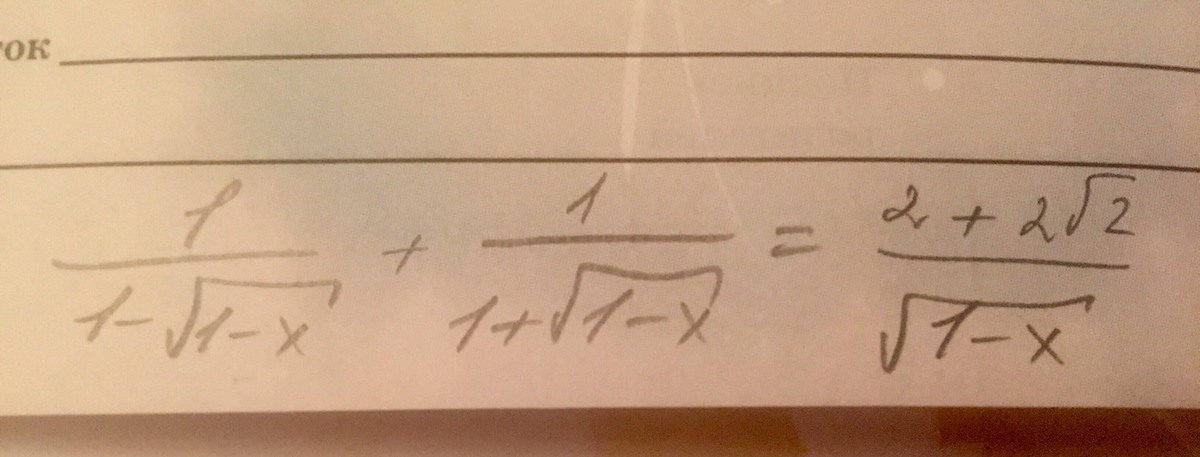

    question img

Ответы 2

  • спасибо!!!
  • \frac{1}{1- \sqrt{1-x} } -\frac{1}{1+\sqrt{1-x}} = \frac{2+2\sqrt2}{\sqrt{1-x}} \; , \; \; \; \; \; \left \{ {{1-\sqrt{1-x}e 0} \atop {1-x\ \textgreater \ 0}} ight. \\\\t=\sqrt{1-x}\; \; ,\; \; \frac{1}{1-t}+\frac{1}{1+t}=\frac{2+2\sqrt2}{t}\\\\\frac{1+t+1-t}{1-t^2}-\frac{2+2\sqrt2}{t}=0\; ;\; \; \frac{2}{1-t^2}-\frac{2+2\sqrt2}{t}=0\\\\\frac{2t-2-2\sqrt2+2t^2-2\sqrt2t^2}{t(1-t^2)}=0\\\\\frac{(2-2\sqrt2)t^2+2t-(2+2\sqrt2)}{t(1-t^2)}=0\\\\\frac{(1-\sqrt2)t^2+t-(1+\sqrt2)}{t(1-t^2)}=0\; \; \to \left \{ {{(1-\sqrt2)t^2+t-(1+\sqrt2)=0} \atop {t(1-t^2)e 0}} ight. \\\\D=1-4(1-\sqrt2)(1+\sqrt2)=1-4(1-2)=5\\\\t_1=\frac{-1-\sqrt5}{2(1-\sqrt2)}=\frac{(-1-\sqrt5)(1+\sqrt2)}{2(1-2)}=\frac{-1-\sqrt2-\sqrt5-\sqrt{10}}{-2}=\frac{1+\sqrt2+\sqrt5+\sqrt{10}}{2}\\\\t_2=\frac{-1+\sqrt5}{2(1-\sqrt2)}=\frac{(-1+\sqrt5)(1+\sqrt2)}{2(1-2)}=\frac{-1-\sqrt2+\sqrt5+\sqrt{10}}{-2}=\frac{1+\sqrt2-\sqrt5-\sqrt{10}}{2} \sqrt{1-x}=\frac{1+\sqrt2+\sqrt5+\sqrt{10}}{2}\; ,  x=1-\frac{(1+\sqrt2+\sqrt5+\sqrt{10})^2}{4} \sqrt{1-x}=\frac{1+\sqrt2-\sqrt5-\sqrt{10}}{2}\; \; \to \; \; x=1-\frac{(1+\sqrt2-\sqrt5-\sqrt{10})^2}{4}

    • Автор:

      buzz
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years