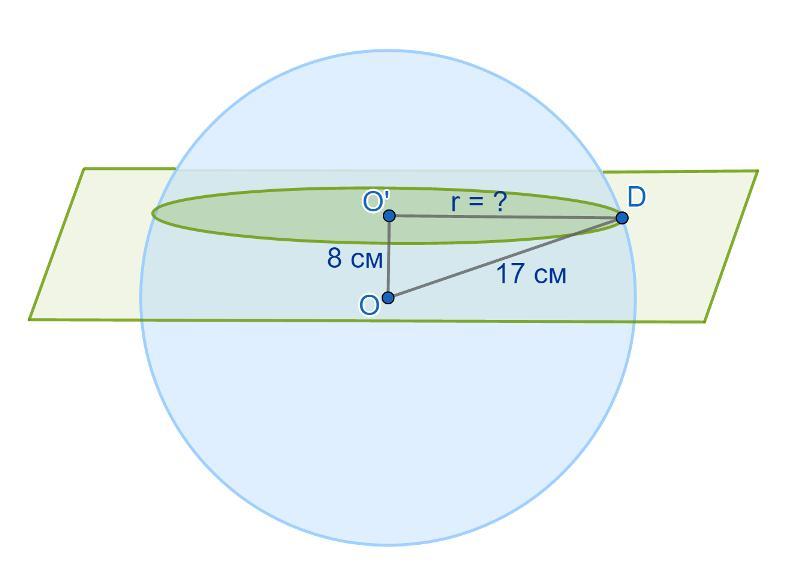
Шар радиуса 17 см пересечен плоскостью, находящейся на расстоянии 8 см от центра. Найдите площадь сечения

Ответ:

Площадь сечения = 225π см².

Пошаговое объяснение:

Сечение шара плоскостью является кругом.

Дано:

Шар с центром в точке O и радиусом  OD = 17 см.

OO' = 8 cм, расстояние от центра шара до секущей плоскости.

Сечение - круг с центром в точке O'.

Найти площадь сечения.

Решение (рисунок прилагается).

Обозначим радиус сечения r.

Расстояние от точки до плоскости является длина перпендикуляра, опущенного из точки на плоскость.

⇒ OO' ⊥ O'D.

⇒ ∠OO'D = 90°.  ΔOO'D прямоугольный, его гипотенузой является радиус шара OD = 17 см, катеты: OO' = 8 см и O'D = r.

Найдем радиус сечения по теореме Пифагора из ΔOO'D:

O'D² = OD² - OO' ;

r² = 17² - 8² = 289 - 64 = 225;

r = 15 см. Радиус сечения = 15 см.

Найдем площадь сечения: Sсеч = πr² = π * 15² = 225π (см²).

Ответ: площадь сечения = 225π см².