Задать вопрос Регистрация
Помочь другим

  • 1) Вычислить интегралы непосредственно:
    2) Вычислить интегралы методом замены переменной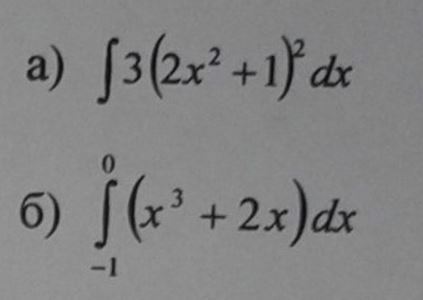

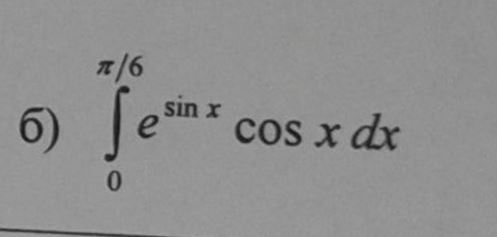
    question img
    question img

Ответы 1

  • 1) a) \int {3(2x^2+1)^2} \, dx=3*\int {(4x^4+4x^2+1)} \, dx=3(4x^5/5+4x^3/3+x)+Cb) \int\limits^0_{-1} {(x^3+2x)} \, dx =x^4/4+x^2|^0_{-1}=0+0-(1/4+1)=-5/42) \int\limits^{ \frac{ \pi }{6} }_0 { e^{sinx} }cosx \, dx Замена sin x = t; dt = cosx dx; t(0) = 0; t(pi/6) = 1/2 \int\limits^{1/2}_0 {e^t} \, dt =e^t|^{1/2}_0=e^{1/2}-e^0= \sqrt{e}-1

    • Автор:

      justice24
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years