-
Обратная матрица. Найти обратную матрицу к матрице А и проверить выполнение равенства. n =4 m =1
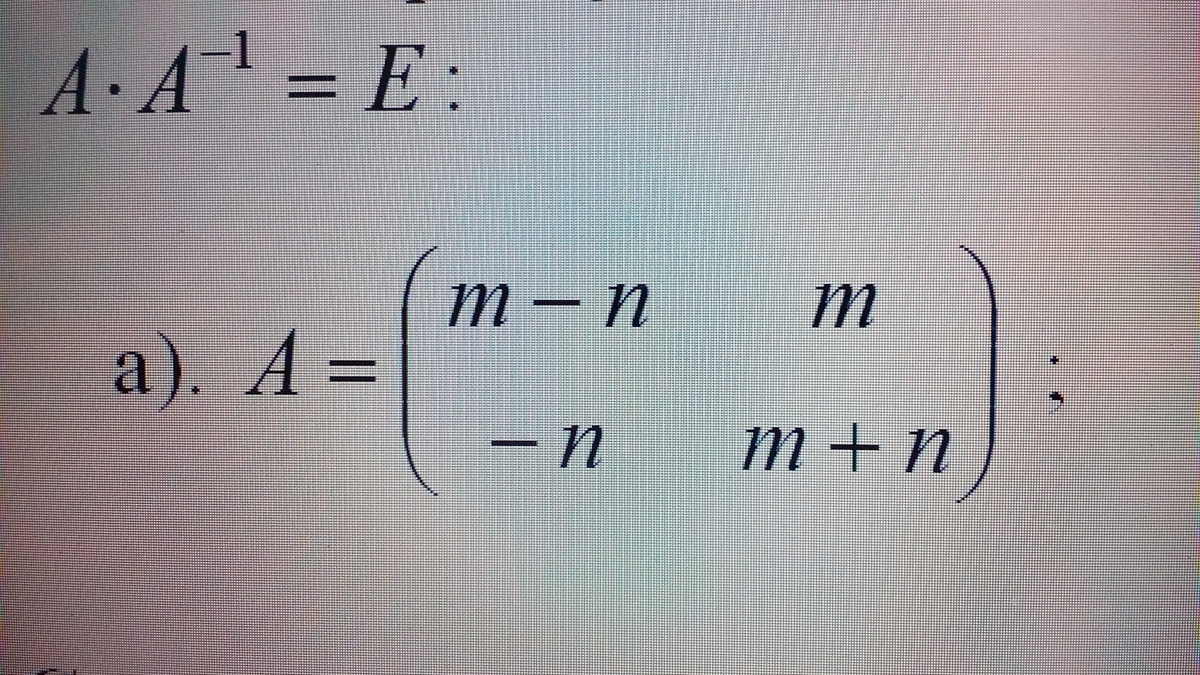
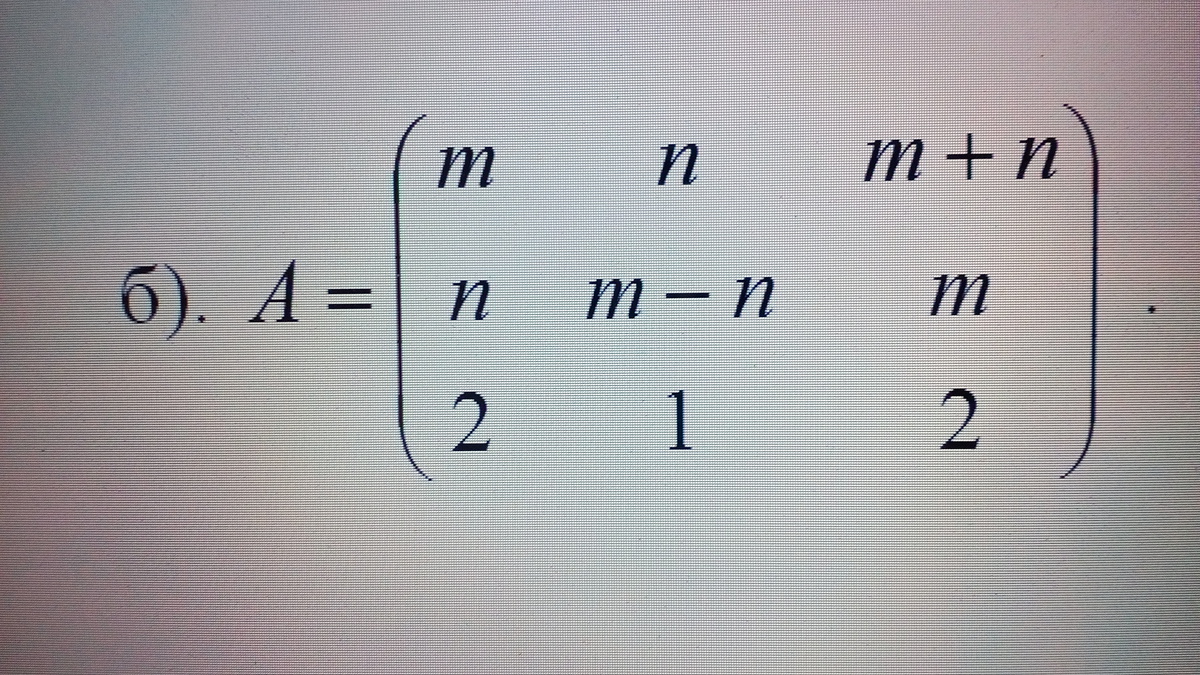
-
Предмет:
Математика -
Автор:
josiepqrw - 6 лет назад
-
Ответы 1
-
(матрица Миноров)
(Матрица алгебраических дополнений.)
(Транспонированная матрица алгебраических дополнений.)Подставляем
Проверять даже смысла нет . Т.к
Это св-во.б) A =
Методом Гаусса ищем обратную
-
Автор:
magdalena - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Начертить три отрезка первый длиной 6 см второй на 3 см короче первого а третий в четыре раза длиннее второго
-
Предмет:
Математика -
Автор:
velascoxc8x - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1) Употребите глагол в нужной форме:
1. My mother (to like) to read romantic books in the evening.
2. We (to visit) Moscow last winter.
3. They (to come) tomorrow in the morning.
4. Не (to want, not) more coffee now.
5. Students (to learn) much at the University every day.
6. I (to read, not) this book when I was a child.
7. My sister (to play) the piano very well when we have guests.
8. Children (to like, not) to go to school every morning.
2) Выберите единственно правильный вариант:
1. We ____ play hockey in summer.
(aren’t/ does/is/ don’t/ have/ doesn’t/ are/ hasn’t)
2. She _____ him in the shop last time.
(see/ doesn’t sees/ sees/ saw/ didn’t saw/ seen/ does)
3. ______ you go to the party yesterday?
(had/ do/ don’t/ have/ shall/ does/ did/ were/ are)
4. He___English very well.
(speaks/ speak/ didn’t speaks/ doesn’t speaks/ don’t speak)
5. your brothers study at the OSU?
(is/ does/ are/ do/ shall/ doesn’t/ was/ will be/ has)
-
Предмет:
Английский язык -
Автор:
adriana23 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
почему во многих крупных городах мира в безветренную погоду людям не хватает кислорода.
-
Предмет:
Окружающий мир -
Автор:
schultzpetty - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Треба написати коротенько міні-твір на тему Знай, Люби, Бережи дерева.Наприклад ;Знай що дерева .............................................,Люби дерева..........................,Бережи .................................Дуже треба .Це на плакат.У 3 стовпчики.
-
Предмет:
Биология -
Автор:
kelsie985p - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
