-
Помогите найти производные и упростить полученные выражения
С решением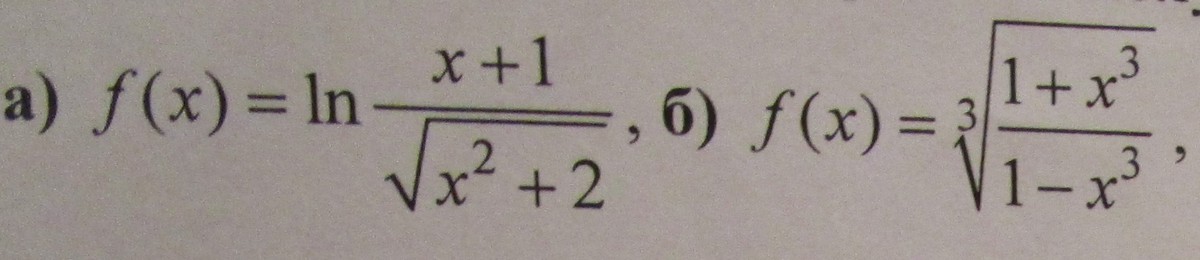
-
Предмет:
Математика -
Автор:
cindyjensen - 6 лет назад
-
Ответы 1
-
а)
б)
-
Автор:
ariaskinner - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- 3 3 3 равно 10 расставить знаки
-
Тригонометрическое неравенство.
Моё решение во вложении, но с ответом из книги не совпадает один знак. В книге не π+2π, а π - 2π. Почему?
Вот другое пример
[tex]sinx(sinx-\frac{1}{2})\ \textless \ 0[/tex]
Решаю с помощью формулы (во втором вложении формулы) и получаю не совсем правильные ответы, а точнее если sinx -
Say what questions the pupils asked at the meeting with Brian Kelly, a Hollywood actor. Example: Mark wondered how long Brian had been working in cinema. Mark: How long have you been working in the cinema? 1) Linda wanted to know if Brian had ever taken part in film festivals in Cannes [kaen], France. 2) Diana asked if Brian himself often went to the cinema. 3) Greg asked if Brian had been keeping to a diet of fruit and vegetables. 4) Susan wanted to know when Brian had been to the theatre last. 5) Jack wondered with how many directors Brian had worked. 6) Kevin asked who Brian’s favourite director was. 7) Julie wanted to know when Brian had begun his career. 8) Sarah asked if Brian was going to visit some European countries. 9) Sam wondered in how many films Brian had appeared.
-
Предмет:
Английский язык -
Автор:
kenyonks37 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1/3 метров сколько будет сантиметров
-
Предмет:
Математика -
Автор:
salomón - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
