Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста решить,с подробными ответами.Заранее спасибо

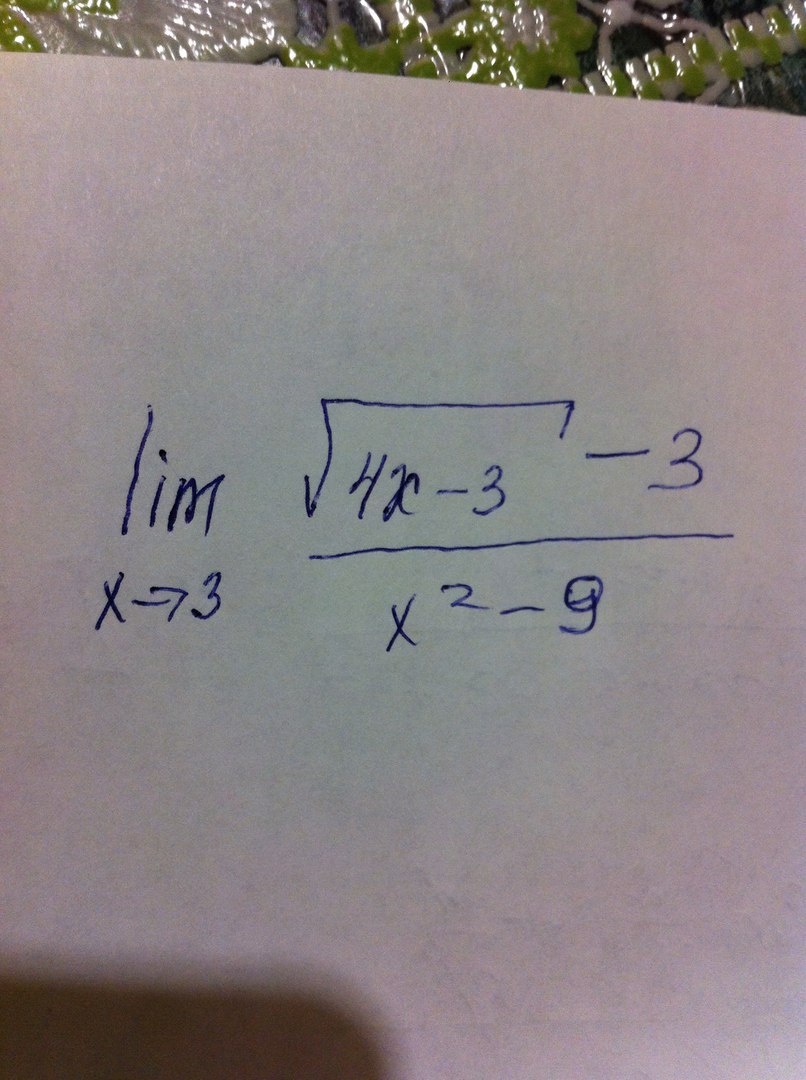
    question img
    question img

Ответы 1

  • 1) \lim_{x \to 3} \frac{ \sqrt{4x-3} -3}{x^2-9}= \lim_{x \to 3} \frac{ (\sqrt{4x-3} -3)(\sqrt{4x-3} +3)}{(x-3)(x+3)(\sqrt{4x-3} +3)}= =\lim_{x \to 3} \frac{ 4x-3-3^2}{(x-3)(x+3)(\sqrt{4x-3} +3)}=\lim_{x \to 3} \frac{ 4(x-3)}{(x-3)(x+3)(\sqrt{4x-3} +3)}==\lim_{x \to 3} \frac{ 4}{(x+3)(\sqrt{4x-3} +3)}= \frac{4}{(3+3)( \sqrt{4*3-3}+3 )} = \frac{4}{6*6}= \frac{1}{9} 2) Точки разрыва: проверяем x = 0 и x = 2x = 0: \lim_{x \to 0-0} (x-3)=0-3=-3 - предел слева \lim_{x \to 0+0} (x^2 - 2)=0-2=-2 - предел справаx = 2 \lim_{x \to 2-0} (x^2-2)=2^2-2=2 - предел слева \lim_{x \to 2+0} (3-x)=3-2=1 - предел справаГрафик рисуйте сами. Он будет из 3 кусков:При x < 0 - прямая y = x - 3При 0 <= x <= 2 - парабола y = x^2 - 2При x > 2 - прямая y = 3 - x

    • Автор:

      joel10
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years