-
вычислить производную высшего порядка заданной функции
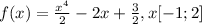
-
Предмет:
Математика -
Автор:
raven - 6 лет назад
-
Ответы 3
-
спасибо огромное)
-
Автор:
jamesoncross - 6 лет назад
-
0
-
-
Производные высших порядков: f''(x) = 6x^2; f'''(x) = 12x; f(iv)(x) = 12; f(v)(x) = 0
-
Автор:
nikitalozano - 6 лет назад
-
0
-
-
Судя по заданию, здесь надо найти наибольшее и наименьшее значения функции на отрезке.f(x) = x^4/2 - 2x + 3/2; x = [-1, 2]Находим на концах отрезкаf(-1) = 1/2 - 2(-1) + 3/2 = 1/2 + 2 + 3/2 = 4f(2) = 16/2 - 2*2 + 3/2 = 8 - 4 + 3/2 = 5,5Находим точки экстремума. Производную приравниваем к 0.f ' (x) = 4x^3/2 - 2 = 2x^3 - 2 = 2(x^3 - 1) = 0x = 1f(1) = 1/2 - 2*1 + 3/2 = 1/2 - 2 + 3/2 = 0Наименьшее значение: f(1) = 0Наибольшее значение f(2) = 5,5
-
Автор:
yaelko2s - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Прочитай. Докажи,чтоперед тобой тексты. Как связаны предложения в тексте?Спиши второй текст. Заверши предложение Это текст,потому что...
-
Предмет:
Русский язык -
Автор:
ford - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
What were the children doing when they got invitation cards?
-
Предмет:
Английский язык -
Автор:
lucy40 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
.К раствору с 14,7г. серной кислоты добавили гидрооксид калия. Найти массу полученной соли.
-
Предмет:
Химия -
Автор:
georginaxlsc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Скорости велосипедиста и пешехода ровные адпаведна 15км/г и 5км/г. Велосипелист проехав на 50 км больш за пешехода. Найдите час движения велосипедиста,уличывши, что он у 2 раза большы за час руху пешехода
-
Предмет:
Математика -
Автор:
jasper29 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
