-
Полностью исследуйте функцию 3x/ 1+x^3
схема:
1.Область определения
2.четность, ни четность
3.точки пересечения с осями координат
4. непрерывность
5.монотонность и экстремум
6.выпуклость , вогнутость и перегиб
7.асимптоты (вертик, наклон,горизонт)
8.график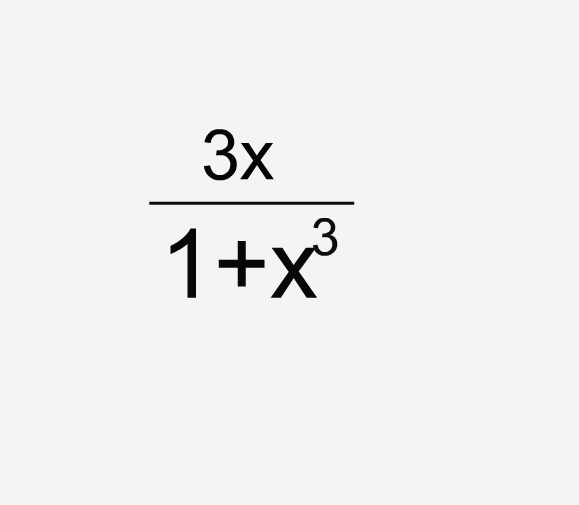
-
Предмет:
Математика -
Автор:
pedro63 - 6 лет назад
-
Ответы 1
-
1.Область определенияD(f)∈(-∞;-1) U (-1;∞)2.четность, ни четность f(-x)=-3x/(1-x³)=-3x/(-(x³-1)=3x/(x³-1) ни четная,ни нечетная3.точки пересечения с осями координат х=0 у=0 (0;0)4. непрерывностьФунция не существует при х=-1⇒прерывна5.монотонность и экстремум f`(x)=(3+3x³-9x³)/(1+x³)²=(3-6x³)/(1+x³)²=03-6x³=0x³=1/2x=1/∛2 + + _---------(-1)-------(1/∛2)---------- maxвозр x∈(-∞;-1) U (-1;1/∛2)убыв x∈(1/∛2;∞)ymax(1/∛2)=2/∛2=∛46.выпуклость , вогнутость и перегибf``(x)=[-18x²(1+2x³+x^6)-(6x²+6x^5)(3-6x³)]/(1+x³)^4==(-18x²-36x^5-18x^8-18x²+36x^5-18x^5+36x^8)/(1+x³)^4==(18x^8-18x^5-36x²)/(x+x³)^4=18x²(x^6-x^3-2)/(1+x³)^4=018x²(x^6-x^3-2)=0x=0x^6-x³-2=0x³=aa²-a-2=0a1+a2=1 U a1*a2=-2a1=-1⇒x³=-1⇒x=-1∉D(f)a2=2⇒x³=2⇒x=∛2 _ _ _ +----------(-1)----------(0)------------(∛2)------------вып вверх вып вверх вып вверх вогн внизy(∛2)=3∛2/(1+2)=∛2 (∛2;∛2)-точка перегиба7.асимптоты (вертик, наклон,горизонт)При х=-1 разрыв,значит х=-1 -вертикальная асимптотаk=limf(x)/x=lim3x/(1+x³)x=lim3/(1+x³)=3/∞=0b=lim(f(x)-kx)=lim(3x/(1+x³)-0*x)=lim3x/(1+x³)=∞/∞=lim(3/x²)/(1/x³+1)==0/1=0Наклонных асиптот нет8.график
-
Автор:
gypsy - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите пожалуйста! Встявляя пропущенные буквы и знаки препинания:
1. На занятиях по воен...ой подготовке старш...клас...ники стреляли из положения лежа по круглым мишеням.
2. Вечером лежа в п...стели мальчик вспоминал события м..нувшего дня.
3. Проезд в м...ршрутном такси стоя запрещ...н.
4. Куда перем...ститься это изобр...жение, если он будет наблюдать стоя?
5. Мальчики стоя на носу лодок держ...т концы легкой в...ревки протянут...й между лодками.
-
Предмет:
Русский язык -
Автор:
lorenzo91 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
дано 4 спички , раставленные в форме плюса (+)
вам нужно переставить одну спичку так , чтобы получился квадрат
переставить можно только одну спичку
"ps: делать нечего. решил вам подкинуть голлволомку на последние балы"-
Предмет:
Другие предметы -
Автор:
admiralrodriguez - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
как решить 4*3• 2*=*83+***=****
-
Предмет:
Математика -
Автор:
mitchell170 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Вспомните и запишите два фразеологизма в состав которых входит числительные
-
Предмет:
Русский язык -
Автор:
jeffrey819 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
