-
Найдите наибольшее значение функции на промежутке от 0 до п/2
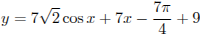
-
Предмет:
Математика -
Автор:
mariannapace - 6 лет назад
-
Ответы 1
-
*знак корня обозначим как v для удобства
1. Найдём производную функции: y' = -7*v2*sin(x) + 7
2. Рассмотрим значения производной на границах интервала:
y' (0) = -7*v2*sin(0) + 7 = 0 + 7 = 7
y'( п/2) = -7*v2*sin(п/2) + 7 = 7 - 7*v2= -7*(v2 - 1)
Таким образом, функция в начале интервала возрастает, а в конце убывает. Следовательно, наибольшее её значение будет находится в пределах интервала, там, где производная равна нулю
3. Составим уравнение по этому условию:
y' = -7*v2*sin(x) + 7 = 0
7 = 7*v2*sin(x)
sin(x) = 1/v2
x = п/4
Мы нашли точку, в которой значение функции будет наибольшим
5. Подставим эту точку в выражение функции:
y (п/4) = 7*v2*cos(п/4) + 7*п/4 - 7*п/4 + 9 = 7*v2*1/v2 + 9 = 7 + 9 = 16
Общий ход решения такой, числа, надеюсь, верные получились
-
Автор:
moreno - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Помогите пожалуйсто
Вот тема Что обозначает глагол по этой теме нужно ответить на вопросы помогите пожалуйсто
1) Какие грамматические ( морфологические) признаки имеет глагол? Как он изменяется?
2) По какой морфеме можно определить морфологические признаки глагола?
-
Предмет:
Русский язык -
Автор:
drake - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
помогите разобрать по составу слово отсутствие, возвратился, вытекал,
-
Предмет:
Русский язык -
Автор:
cheese49 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Квадратную коробку наполнили одинаковыми квадратными шоколадками. Кирилл съел все 20 шоколадок верхнего слоя,которые лежали вдоль стенок коробки. Сколько шоколадок осталось в коробке?
-
Предмет:
Математика -
Автор:
kirbyhouston - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
О какой звезде идёт речь в стихотворении Н. М. Рубцова "Звезда полей"????? Очень надо подскажите, пожалуйста!!!!!!!!!
-
Предмет:
Литература -
Автор:
captainhart - 6 лет назад
-
Ответов:
1 -
Смотреть
-
