-
Я гуманитарий)Очень нужна помощь. Помогите решить уравнения и неравенства. Заранее спасибо.
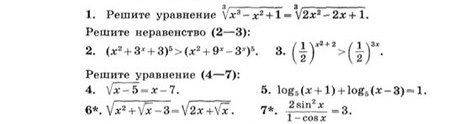
-
Предмет:
Математика -
Автор:
harrison83 - 6 лет назад
-
Ответы 1
-
1.∛(x³-x²+1) =∛(2x²-2x+1) ;x³-x²+1 =2x²-2x+1 ;x³-3x²+2x =0 ;x(x² -3x+2) =0 ;x=0; илиx² -3x+2 =0 ⇒ x =1 ; x=2.ответ : { 0; 1;2} .* * * одно из этих чисел * * *-------2.(x² +3^x +3)⁵ > (x²+9^x -3^x)⁵ ;x² +3^x +3 > x²+9^x -3^x ;9^x -2*3^x-3=0 ;(3^x)² -2*3^x-3=0 ; * * * замена t =3^x >0 * * *t² -2t -3 =0 ;t₁= -1 не решения t₂= 3 ⇒3^x =3 ⇒x =1. ответ : 1 .-------3.(1/2)^(x²+2) >(1/2)^(2x) ;x²+2 < 2x ;x²-2x+2 < 0 ;(x-1)² +1 < 0 ⇒ x ∈ ∅ (пустое множество) т.к. левая часть неравенства положительно (вернее не меньше 1) .ответ : ∅.-------4.√(x-5) = x -7 ; * * * x -7 ≥0 * * *x-5 =(x- 7)² ;x² -15x +54=0 ;x₁= 6 не решения x₂ =9.ответ : 9.-------5.Log_5 (x+1) + Log_5 (x-3) =1 ; * * * ОДЗ : { x+1 >0 ; x-3>0.⇔x>3. * * *(x+1)(x-3) =5 ;x² -2x -8 =0;x₁= -2 не решения x₂ =4.ответ : 4.-------6. √(x²+√x -3) =√ (2x +√x) ; * * * ОДЗ : { x≥0 ; x²+√x -3 ≥0. * * *x²+√x -3 =2x +√x ;x²-2x -3 =0 ;x₁= -1 ∉ ОДЗ x₂ =3.ответ : 3.-------7.2sin²x/(1-cosx) =3 ; * * * ОДЗ : 1-cosx ≠0⇔cosx≠1 * * *2(1-cos²x)/(1-cosx) =3 ;2(1+cosx)(1-cosx) /(1-cosx) =3 ; * * * 1-cosx ≠ 0 * * *2(1+cosx) =3 ;2cosx =1 ;cosx =1/2 ;x =±π/3 +2πn , n ∈Z.ответ : ±π/3 +2πn , n ∈Z.---------------Удачи !
-
Автор:
kiraconley - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите пожалуйста решить неравенство,заранее спасибо
-
Предмет:
Алгебра -
Автор:
pretty ladygwkk - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
чего люди обычно используют ноутбук полный ответ
-
Предмет:
Окружающий мир -
Автор:
boy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какое минимальное число фосфолипидных мембран пересекает молекула кислорода, проникая из полости альвеолы легкого в эритроцит легочного капилляра?
-
Предмет:
Биология -
Автор:
brendan293 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
найдите сумму первых пяти членов геометрической прогрессии(bn), у которой b1=14,q=1/2. С объяснением.
-
Предмет:
Математика -
Автор:
joe85 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
