-
Восстанови функции используя данные её производных, изображенных на графиках в приложении.
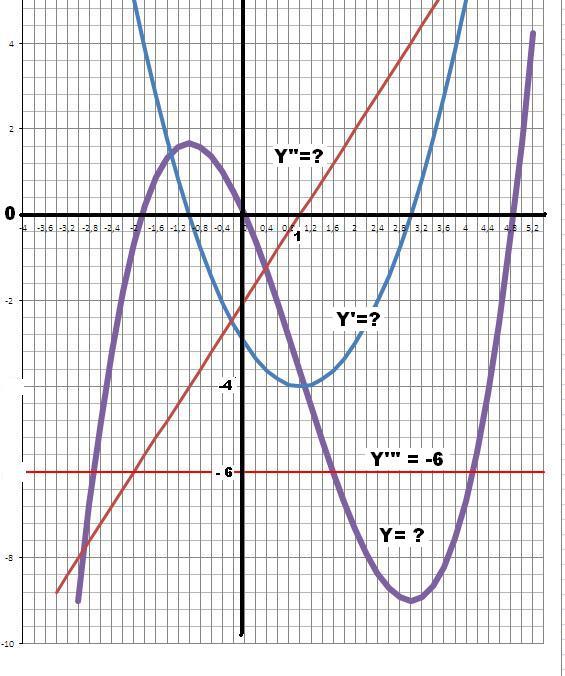
-
Предмет:
Математика -
Автор:
peter197 - 6 лет назад
-
Ответы 6
-
ДАНО - 3-я Y''' = -6 ДАНО
-
Автор:
kylie61 - 6 лет назад
-
0
-
-
Ну давайте тогда удалим вашу задачу :–)
-
Автор:
banjocook - 6 лет назад
-
0
-
-
Я могу написать 0*x=6.
-
Автор:
adón29 - 6 лет назад
-
0
-
-
Тоже будет "ДАНО" :–))))
-
Автор:
oprahst8m - 6 лет назад
-
0
-
-
С благодарностью. раз есть ПРИНЦИПИАЛЬНЫЕ ОШИБКИ. Эту линию чертил "от руки" и наклон не тот и сдвиг.
-
Автор:
marlie - 6 лет назад
-
0
-
-
Вторая производная – прямая, задаваемая линейной функцией, имеет точки пересечения с осями Ox и Oy: ( 1; 0 ) и ( 0; –2 ) – соответственно:Уравнение линейной функции
Составим систему уравнений,подставив в уравнение прямой две указанные выше точки:
Итак, уравнение второй производной:
Заметим, что третья производная будет иметь уравнение:
что точно не соответствует графику
а поэтому будем считать график
для третьей производной – данным в задании ошибочно.Первая производная является одной из первообразных с неопределённым слагаемым для второй производной, а поэтому находится интегрированием:
При x = 0, что видно по графику:
Т.е.:
Итак, уравнение первой производной:
Функция является одной из первообразных с неопределённым слагаемым для своей производной, а поэтому находится интегрированием:
При x = 0, что видно по графику:
Т.е.:
Итак уравнение функции:
О т в е т :
*** Если считать, что третья производная дана не "по ошибке", то у задачи НЕ СУЩЕСТВУЕТ решений.
-
Автор:
jaxsonbrock - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Қай сөзге б әрпін қоямыз?
Кіта.., ғажа..,до..ы, кет..ең-
Предмет:
Қазақ тiлi -
Автор:
sammyf1sy - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Запишите периодическую дробь в виде обыкновенной:
А)1,0(1) б)1,5(4) в)8,7(5) г)-3,(31) д)2,2(02) е)0,(123)
Например: 0,3
x=0,3
10x=3,3
9x=3
x=3\9=1\3
Дам 30 баллов-
Предмет:
Математика -
Автор:
johannatljk - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Вопрос 14
Четверо одноклассников решили купить подарок классному руководителю на день рождения. Первый заплатил треть суммы, вносимой остальными; второй –
1/4 часть суммы, вносимой остальными; третий – 1/5
суммы, вносимой остальными, а четвертый – 4600 рублей. Сколько стоит подарок?
(Ответ запишите числом в рублях). -
аргументы из литературы на тему "глаза-зеркало души " Только Войны и Мир не брать в пример
-
Предмет:
Литература -
Автор:
dee dee65xq - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
