Задать вопрос Регистрация
Помочь другим

  • помогите с решением тригонометрического уравнения ( напишите пожалуйста как решали)

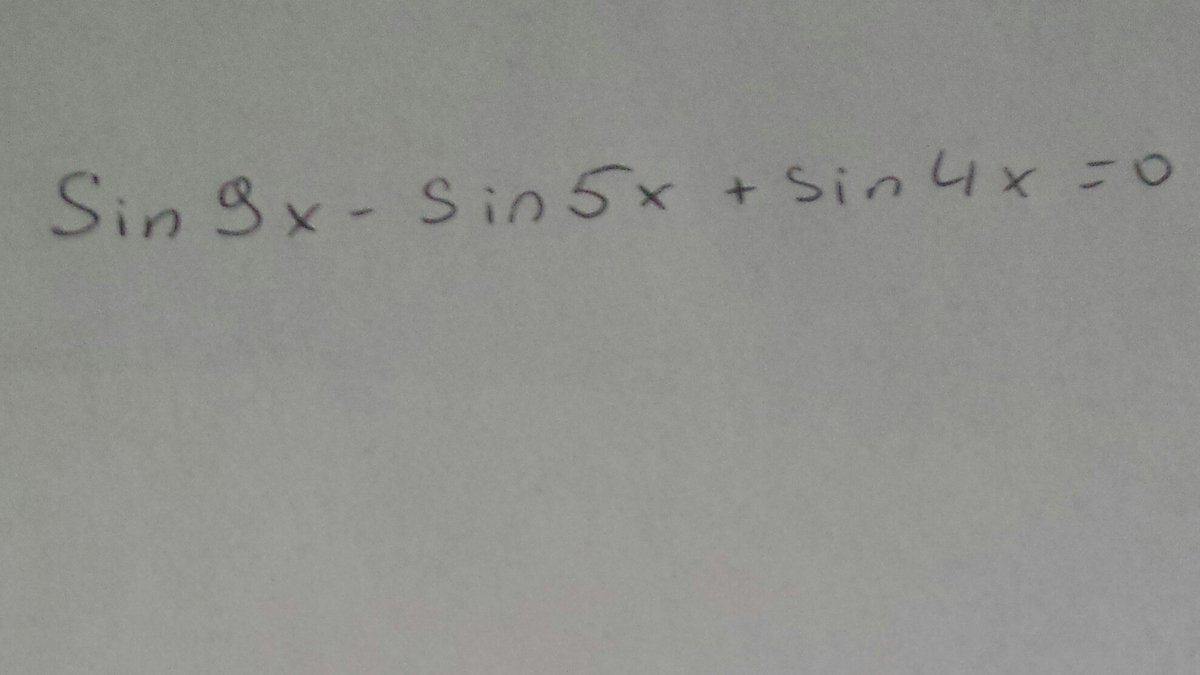
    question img

Ответы 2

  • Почему выражение 2sina*cosa подставляем вместо sin4x?

    • Автор:

      codi4sfs
    • 6 лет назад
    • 0
  • Уравнение решается преобразованием суммы или разности тригонометрических функций в произведение. Воспользуемся формулойsin \alpha -sin \beta =2sin \frac{ \alpha - \beta }{2}cos \frac{ \alpha + \beta }{2} Получим2sin \frac{9x-5x}{2}cos \frac{9x+5x}{2}+sin4x=0 2sin2x*cos7x+sin4x=0Теперь воспользуемся формулой для синуса двойного углаsin2 \alpha =2sin \alpha *cos \alpha и подставим в наше уравнение вместо sin4x получим2sin2x*cos7x+2sin2x*cos2x=0Выносим 2sin2x за скобки2sin2x(cos7x+cos2x)=0Сумму косинусов в скобках преобразуем в произведение по формулеcos \alpha +cos \beta =2cos \frac{ \alpha + \beta }{2}*cos \frac{ \alpha - \beta }{2} Получим2sin2x(2cos \frac{7x+2x}{2}*cos \frac{7x-2x}{2})=0 Отсюда получаем три уравнения, так как уравнение равно нулю если хотя бы один из множителей равен нулю: \left \{ {{sin2x=0} \atop {cos \frac{9x}{2} =0}} \atop {cos \frac{5x}{2} =0} ight. \left \{ {{2x= \pi n} \atop { \frac{9x}{2} = \frac{ \pi }{2}+ \pi n }} \atop { \frac{5x}{2} = \frac{ \pi }{2}+ \pi n }}ight. \left \{ {{x= \frac{ \pi n}{2} } \atop {x= \frac{ \pi }{9}+ \frac{2 \pi n}{9} }} \atop {x= \frac{ \pi }{5}+ \frac{2 \pi n}{5} }}ight.

    • Автор:

      lokii9z3
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years