-
Решите пожалуйста, срочно нужно)
1.
a) Решите уравнение: sin⁴x+cos⁴x=1-cos²x
б) Найдите все корни этого уравнения, принадлежащие промежутку [π/2;2π]
2.
а) Решите уравнение: sin⁴x+cos⁴x=1-3/2sin²x
б) Найдите все корни этого уравнения, принадлежащие промежутку [π/2;2π]
Заранее благодарен:)
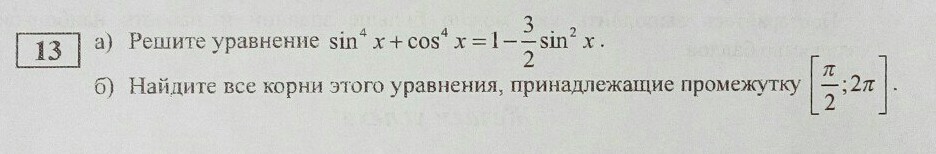
-
Предмет:
Математика -
Автор:
maddygrimes - 6 лет назад
-
Ответы 2
-
Спасибо преогромнейшее! Очень выручил:)
-
Автор:
bryancruz - 6 лет назад
-
0
-
-
1.sin⁴x + cos⁴x = 1 - cos²x, x ∈ [π/2; 2π]sin⁴x + cos⁴x = sin²xsin²x·(sin²x - 1) + cos⁴x = 0 cos⁴x - sin²x·cos²x = 0cos²x·(cos²x - sin²x) = 0cos²x · cos 2x = 0cos x = 0 или cos 2x = 0x = π/2 + πk, k ∈ Z 2x = π/2 + πn, n ∈ Z x = π/4 + πn/2, n ∈ ZНа указанном промежутке: x ∈ {π/2; 3π/4; 5π/4; 3π/2; 7π/4}.2.sin⁴x + cos⁴x = 1 - 3/2·sin²x, x ∈ [π/2; 2π]2sin⁴x + 2cos⁴x = 2 - 3sin²x2sin⁴x + 2cos⁴x = 2cos²x - sin²x2sin⁴x + 2cos⁴x - 2cos²x = -sin²x2sin⁴x + 2cos²x·(cos²x - 1) = -sin²x2sin⁴x - 2sin²x·cos²x = -sin²x2sin²x·(sin²x - cos²x) = -sin²x2sin²x·cos 2x = -sin²xsin²x·(1 + 2cos 2x) = 0sin x = 0 или 1 + 2cos 2x = 0x = πk, k ∈ Z 2cos 2x = -1 cos 2x = -1/2 2x = (+/-) 2π/3 + 2πn, n ∈ Z x = (+/-) π/3 + πn, n ∈ ZНа указанном промежутке: x ∈ {2π/3; π; 4π/3; 5π/3; 2π}.
-
Автор:
onyxsellers - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Пожалуйста ответьте на этот вопрос Если ответите я поставлю Вам 100 баллов Пожалуйста ответьте
-
Предмет:
Математика -
Автор:
stuart70 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Полезные ископаемые Приморского края ?
-
Предмет:
География -
Автор:
alexusliwc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Разбери. По членам предложения и части речи над дальними болотами кружили стаи птиц
-
Предмет:
Математика -
Автор:
alirubio - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
игры плюс 27 игрек равно 0,952
-
Предмет:
Математика -
Автор:
miranda54 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
