-
Решите уравнение и выберите верный ответ
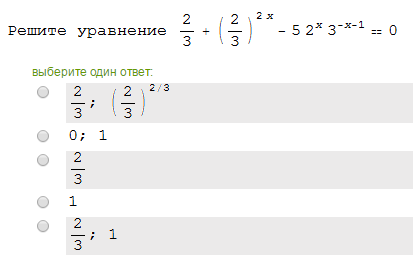
-
Предмет:
Математика -
Автор:
preciousvalentine - 6 лет назад
-
Ответы 2
Еще вопросы
-
1955 на казахском прописью
-
Предмет:
Қазақ тiлi -
Автор:
melodycurtis - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Вычислите
[tex] \frac{log_427}{log_43} [/tex]-
Предмет:
Алгебра -
Автор:
rosaliafitzgerald - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
5. В каком варианте ответа правильно указаны все цифры, на месте которых в предложении должны стоять запятые?
Воробей (1) неожиданно взлетев (2) исчез в светлой зелени сада(3) прозрачно сквозившей (4) на предвечернем небе.
1)1,3 2)1,2,3 3)2,3,4 4)2,4
-
Предмет:
Русский язык -
Автор:
alysonconner - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
найти значение выражения (b-300):4,если b=316,332,340,400,500
-
Предмет:
Математика -
Автор:
brennan - 6 лет назад
-
Ответов:
8 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
