-
Отдам 25 баллов
Решить неравенство , фото прикрепляю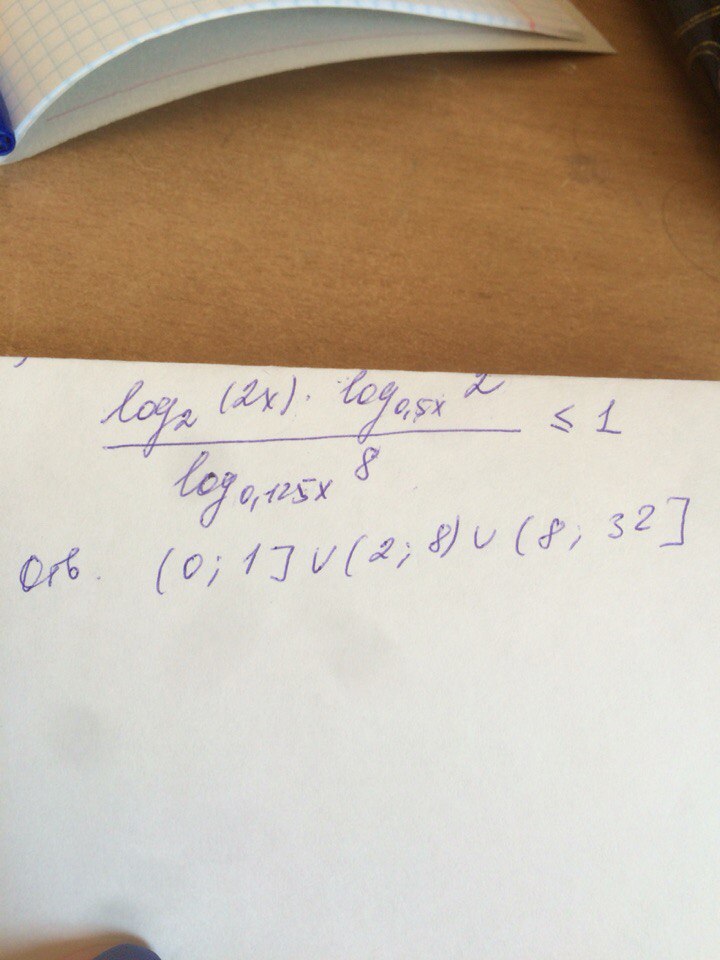
-
Предмет:
Математика -
Автор:
semaj - 6 лет назад
-
Ответы 1
-
Соединим ODZ и решение
-
Автор:
isabellenorton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Поверхность бассейна имеет форму прямоугольника.Длина бассейна 9м,а ширина в 2раза больше.Достаточно ли 1820 квадратных плиток со стороной 30 см,чтобы выложить ими дно бассейна?
-
Предмет:
Математика -
Автор:
goon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
фонетический разбор слова спасибо
-
Предмет:
Русский язык -
Автор:
frost - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
(5/9-11/12)*3 9/12 + (0.3125+5/24)*4 4/5 пожалуйста очень надо
-
Предмет:
Математика -
Автор:
ciscoug7p - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Для приготовления мороженого берут 10 частей воды. З части молочного жира и 5 частей Сахара ( по массе). Сколько потребуется каждого ингридеента что бы приготовить 8242,2 кг мороженого
-
Предмет:
Математика -
Автор:
harley86 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
