Помогите, пожалуйста, решить комбинированный №15 из ЕГЭ по математике (бывш.

Помогите, пожалуйста, решить комбинированный №15 из ЕГЭ по математике (бывш. С3)
Ответ [tex]3/4\ \textless \ x \leq 7[/tex]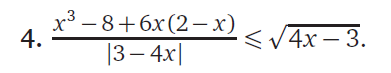
- Предмет:
  Математика
- Автор:
  douglasvhqk
- 6 лет назад

Ответы 1

*Не думаю что это решение лучшее, но другого я просто не увидел.Найдем ОДЗ: $4x-3 \ \textgreater \ 0$ $x \ \textgreater \ \frac{3}{4}$ Исходя из данных ограничений, можно открыть модуль и переписать неравенство в другом виде: $\frac{{x^3-8+6x(2-x)} }{4x-3} \leq (4x-3)^{1/2}$ Числитель дроби можно преобразовать: $x^3-8+6x(2-x)=(x-2)(x^2+2x+4-6x)=(x-2)^3$ Таким образом мы пришли к этому: $\frac{(x-2)^3}{4x-3} \leq (4x-3)^{1/2}$ Перенесем все в одну часть, внесем под один знаменатель: $\frac{(x-2)^3-((4x-3)^{1/2})^3}{4x-3} \leq 0$ Раскроем числитель как разность кубов: $\frac{((x-2)- \sqrt{4x-3})((x-2)^2-(x-2)\sqrt{4x-3}+4x-3)}{4x-3} \leq 0$ Попробуем решить это неравенство методом интервалов, т.е. для начала найдем нули функции:1) $(x-2)- \sqrt{4x-3}=0$ $\left \{ {{(4x-3)=(x-2)^2} \atop {x \geq 2}} ight.$ Единственное решение $x=7$ (и второе решение не влияет на знак неравенства, положительно)2) $(x-2)^2-(x-2)\sqrt{4x-3}+4x-3=0$ $\left \{ {{4x-3=(x-2)^2+2(x-2) \frac{4x-3}{x-2} +(\frac{4x-3}{x-2})^2} \atop {(x-2)+\frac{4x-3}{x-2} \geq 0}} ight.$ После частичного упрощения верхнего уравнения системы получим: $\left \{ {{-x^2-1=(\frac{4x-3}{x-2})^2} \atop {x\geq 2}} ight.$ Дальше решать смысла нет, т.к. верхнее уравнение не будет иметь решений (левая часть равенства всегда отрицательна, правая - положительна)Одновременно с этим знак выражения $(x-2)^2-(x-2)\sqrt{4x-3}+4x-3$ на допустимом (ОДЗ) интервале всегда положителен, поэтому оно никак не влияет на знак неравенства.*Тогда все наше первоначальное неравенство эквивалентно данному: $\frac{x-7}{4x-3} \leq 0$ Его решением и будет являться (с учетом ОДЗ) $\frac{3}{4} \ \textless \ x \leq 7$ * Можно обосновать так: $a^2-ab+b^2= \ \textgreater \ (\frac{a}{b} )^2-(\frac{a}{b})+1$ (в нашем случае уместно) $D\ \textless \ 0$ , коэффициент при числе в квадрате положителен, значит и все значения функции на интервале ОДЗ положительны.
- Автор:
  clark6
- 6 лет назад
- 0
Добавить свой ответ