-
Решить систему методом Крамера и средствами матричного исчисления.
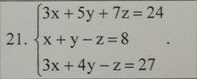
-
Предмет:
Математика -
Автор:
macey - 5 лет назад
-
Ответы 1
-
-
Автор:
midnightkeith - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
решите уравнение
10y+2x(7y-2)=5x(4y+3)+3y-
Предмет:
Математика -
Автор:
athena87 - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
мини соченение на тему Терпение и труд все перетрут,Какого человека ты назавёшь счастливым
-
Предмет:
Русский язык -
Автор:
isabellar4q0 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочините пожалуйста 3 Трёхстишия (ХОККУ). Не берите из интернета и книг пожалуйста. (30 баллов)
-
Предмет:
Литература -
Автор:
cristian33 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
1/9;25/32;3/4;8/13;12/23
в порядке убывания
-
Предмет:
Математика -
Автор:
brenton - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
