-
Интегралы! Помогите пожалуйста! Это очень срочно!
Для того чтобы увеличить изображение, кликните на него (если кто не знает как его увеличивать) Даю 42 бала!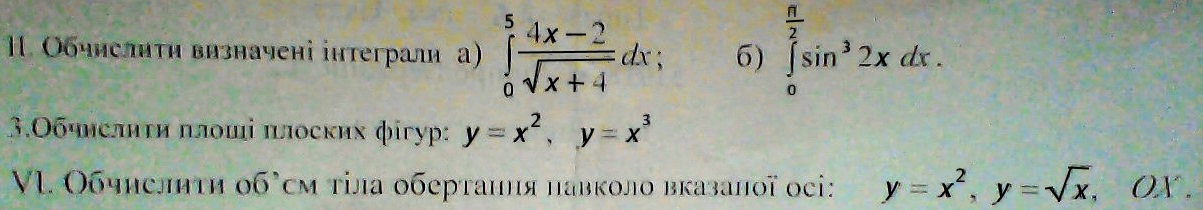
-
Предмет:
Математика -
Автор:
bandit8 - 6 лет назад
-
Ответы 2
-
Спасибо ОГРОМНОЕ!!!!
-
Автор:
conductor - 6 лет назад
-
0
-
-
-
Автор:
toribiogill - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какое слово состоит из приставки, корня, двух суффиксов и окончания? 1) Приморье; 2) загорелый; 3) завистливый; 4) пренебрегать.
-
Предмет:
Русский язык -
Автор:
mosheo7hm - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Решите пожалуйста 212 пример, буду благодарен за помощь
-
решить пример с дробями 1 целая 4/9 +2 целых 5/18
-
Предмет:
Математика -
Автор:
bria - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сочинение скоро каникулы зимние
-
Предмет:
Русский язык -
Автор:
abdielcarney - 6 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
