Задать вопрос Регистрация
Помочь другим

  • Пожалуйста очень нужно, решите на листе. Задание В) Г) Д). Если что-то не видно пишите в коментарии

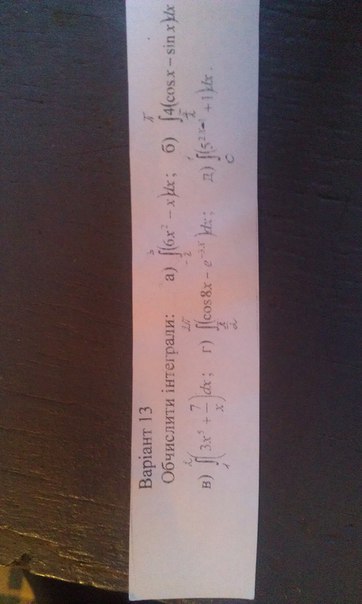
    question img

Ответы 2

  • 1x^6/2+7lnx|2-1=32+7ln2-0,5-7ln1=31,5+7ln2-0=31,5+7ln221/8*sin8x+1/(3e^3x)|2π-π/2=1/8*sin16π+1/(3e^6π)-1/8*sin4π-1/(3e^1,5π)==1/8*0+1/(3e^6π)-1/8*0-1/(3e^1,5π)=(1-e^4π)/3e^6π 31/2ln5*5^(2x-1)+x|1-0=5/(2ln5)+1-1/10ln5=12/5ln5 +1
  • 1. \int\limits^2_1 {3x^5+ \frac{7}{x} } \, dx = (0.5 x^{6} +7ln(x)) = 0.5*64 + 7ln(2) - 0.5 - 0 = 31.5 + 7ln(2)2. \int\limits{cos(8x)- e^{-3x} } \, dx = \frac{1}{8} \int\limits {cos(8x)} \, d(8x) + \frac{1}{3} \int\limits { e^{-3x} } \, d(-3x) = \frac{1}{8}sin(x) + \frac{1}{3} e^{-3x} = \frac{1}{8}(sin(16 \pi )-sin(4 \pi )) + \frac{1}{3}( e^{-6 \pi }- e^{-1.5 \pi } ) = \frac{1}{3}( e^{-6 \pi }- e^{-1.5 \pi })3. \int\limits^1_0 { 5^{2x-1} +1} \, dx = \frac{1}{2} \int\limits^1_0 { 5^{2x-1} } \, d(2x-1) + 1 - 0 = \frac{ 5^{2x-1} }{2ln(5)} +1= \frac{5-0.2}{2ln5} +1 = \frac{2.4}{ln5} +1

    • Автор:

      whitaker
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years