-
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!КТО СМОЖЕТ!!!Исследовать на сходимость числовой ряд
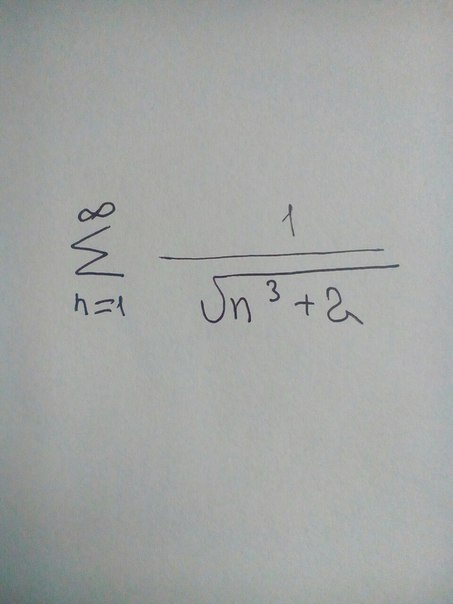
-
Предмет:
Математика -
Автор:
abril - 6 лет назад
-
Ответы 1
-
Так как при любом n √(n³+2)>√n³, то члены данного ряда меньше соответствующих членов ряда с n-ным членом An=1/√n³. Поэтому если ряд ∑1/√n³ сходится, то сходится и данный ряд. Исследуем ряд ∑1/√n³ с помощью интегрального признака Коши. Так как функция f(x)=1/√x³ непрерывна и монотонно убывает в интервале (1;∞), то ряд ∑1/√n³ сходится, если сходится интеграл ∫f(x)*dx=∫dx/√x³, взятый на интервале (1;∞), и расходится, если этот интеграл расходится. Первообразная F(x)=∫dx/√x³=-2/√x, тогда F(∞)-F(1)=0-(-2/√1)=2. Значит, ряд ∑1/√n³ сходится, а вместе с ним сходится и данный ряд.Ответ: ряд сходится.
-
Автор:
mauricio721 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите пж решить задачу 10 буду ооочень благодарна если поможите плз помгите
-
Предмет:
Математика -
Автор:
sarah9 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
разложить на множители х^2-4m-m^2-4
-
Предмет:
Математика -
Автор:
banjo - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
Помогите с переводом (используя герундий)! Буду благодарна! :))
Translate the following sentences into English using the Gerund.
1. Она бросила курить.
2. Они начали играть в шахматы час назад.
3. Он начал водить машину, когда ему было 18 лет.
4. Мы отложим обсуждение доклада.
5. Наконец, они перестали смеяться.
6. Она отрицала, что украла деньги.
7. Нам пришлось отложить поездку на дачу до следующей субботы.
8. Простите, что я потерял вашу ручку.
9. Когда она закончит писать сочинение?
10. Я не возражаю против того, чтобы остаться дома и поработать над моей новой книгой.-
Предмет:
Английский язык -
Автор:
ziggyl8nv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
найти целые положительные значения x удовлетворяющие неравенству
[tex] \frac{5x+1}{x-1} \ \textgreater \ 2x+2[/tex]-
Предмет:
Алгебра -
Автор:
zachariah7f3u - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
