-
Срочно. 3 задания. Помогите решить пожалуйста подробно.
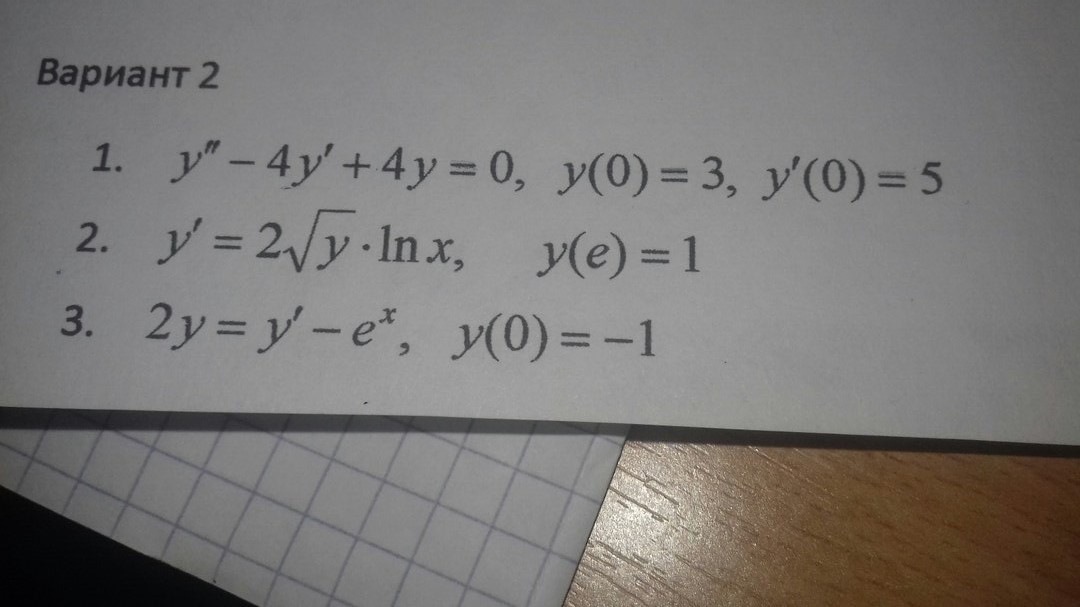
-
Предмет:
Математика -
Автор:
mcmahon - 5 лет назад
-
Ответы 1
-
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.Решение уравнения будем искать в виде y = e^(rx). Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:r² -4 r + 4 = 0D = (-4)² - 4 • 1 • 4 = 0r1 = (-(-4))/(2*1) = 2.Корни характеристического уравнения:Корень характеристического уравнения r1 = 2 кратности 2.Следовательно, фундаментальную систему решений составляют функции:y1 = e2xy2 = xe2xОбщее решение однородного уравнения имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Найдем частное решение при условии: y(0) = 3, y'(0) = 5Поскольку y(0) = c1, то получаем первое уравнение:c1 = 3Находим первую производную:y' = 2 • c1 • e2 • x+2 • c2 • x • e2 • x+c2 • e2 • xПоскольку y'(0) = 2 • c1+c2, то получаем второе уравнение:2 • c1+c2 = 5В итоге получаем систему из двух уравнений:c1 = 32 • c1+c2 = 5т.е.:c1 = 3, c2 = -1Тогда частное решение при заданных начальных условиях можно записать в виде:
-
Автор:
morenoern9 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какие числа называются натуральными ? Назовите все цифры.Назовите разряды в классе единиц.Назовите первые четыре класса в записи натуральных чисел.
-
Предмет:
Математика -
Автор:
dozer - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста 22 номер
Заранее огромное спасибо))-
Предмет:
Алгебра -
Автор:
shannon8dyj - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
В шестых классах 36 мальчиков и 42 девочки. Сколько существует возможностей создать группы учащихся так, чтобы во всех группах было по одинаковому числу
девочек и по одинаковому числу мальчиков? Какое может быть наибольшее число таких групп?-
Предмет:
Математика -
Автор:
jessiepatrick - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Как из хлората калия получить хлор?
How much to ban the user?
1 hour
1 day
100 years
