-
решите неравенство
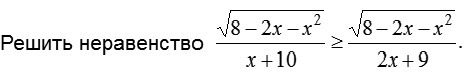
-
Предмет:
Математика -
Автор:
adrianmorris - 6 лет назад
-
Ответы 7
-
Что за дичь?
-
Автор:
verónicamdxc - 6 лет назад
-
0
-
-
а в чем собственно проблема? одз неверно?
-
Автор:
nathaniel - 6 лет назад
-
0
-
-
Ну как тебе сказать. Все что написано - бред. Я вообще не понимаю что ты пытался сделать и зачем.
-
Автор:
cher - 6 лет назад
-
0
-
-
можешь пожалуйста показать свое решение, чтоб я понял в чем ошибка и больше не допускал ее.
-
Автор:
cindytsuc - 6 лет назад
-
0
-
-
Вечерком запощу решение, если больше никто не решит.
-
Автор:
clarahayes - 6 лет назад
-
0
-
-
8-2х-х^2>0 , х1 =-4, х2=2. х+10>0, х1=-10. 2х+9>0 х1 =-4,5 хэ[2,+Бесконечности)
-
Автор:
ethanwilliams - 6 лет назад
-
0
-
-
Разбираемся с ОДЗ. Она задается системой{8-2x-x²≥0{(x+10)(2x+9)≠0Решение системы такое: -4≤x≤2Возвращаемся к неравенству. Корень величина положительная, и на нее можно разделить обе части неравенства перед этим записав его нули x=-4, x=2 (так как знак нестрогий они являются решениями неравенства).Получаем неравенство:
Которое решается методом интервалов и в пересечение с ОДЗ корня дает решение 1≤x≤2Ответ: x ∈ {-4} ∪ [1; 2]
-
Автор:
gaugew1mf - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найдите значение выражения ( оно во вложении).
Закончил школу называется , ума не приложу как это преобразовать-
Предмет:
Математика -
Автор:
mariah93 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Present Simple and Past Simple правила за 5 класс
-
Предмет:
Английский язык -
Автор:
amani - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
знайти площу трикутника дві сторони якого дорівнюють 28 і 30 см, а медіана проведена до 3ої сторони 13 см?
-
Предмет:
Математика -
Автор:
darcy5som - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Перевидите текст пожалуйста!
Work in groups of three or four. Choose one of the texts and read it together. Discuss this questions in your group: What are the most interesting facts you know about this sea animal? Make a fact fil
Text 1.A jellyfish.The jellyfish is the oldest animals in the world.It has lived on our planet since dinosaurs and sharks.Scientists thenk that there are 2,000 kings of jellyfish in the seas.They are made up of 95% water.They can be in different colours: write,blue,green,orange,pink,yellow and others. They have no heart, no bones and no brain. jELLYFISH have umbrella-like bodies,a mouth and tentacles. They use their tentaCLES TO STING their food or to warn other creatures including people if they are afraid of them. Some jellyfish are very dangerous. The box jellyfish is the most dangerous jelly in the world. It lives in Australia. It has enough poison to kill more than 60 people. The crystal jelly has the biggest mouth while the Lion, s Mane is the largest jelly in the world. pEOPLE IN cHINA or in japan sometimes cook jellyfish. The dish is often prepered with vegetable oil,vinegar and sugar or as a salad with vegetables.-
Предмет:
Английский язык -
Автор:
mandy - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
