Задать вопрос Регистрация
Помочь другим

  • При каком наибольшем значении параметра а функция будет непарной?

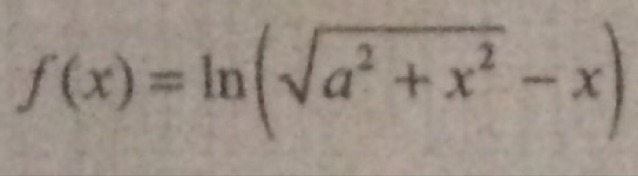
    question img

Ответы 2

  • Функция f(x) непарная (нечетная), если для нее выполняется -f(x)=f(-x).Тогда -ln(√(x²+a²)-x) = ln(√((-x)²+a²)-(-x)).ln(√(x²+a²)+x)+ln(√(x²+a²)-x)=ln(1)ln((√(x²+a²)+x)(√(x²+a²)-x))=ln(1)(√(x²+a²)+x)(√(x²+a²)-x)=1(x²+a²)-x²=1a²=1Наибольшее a=1.

    • Автор:

      pablo20
    • 5 лет назад
    • 0
  • Если функция нечетная, то f(-x) = -f(x)\displaystyle \ln\left(\sqrt{a^2+(-x)^2}-(-x)ight)=-\ln\left(\sqrt{a^2+x^2}-xight) \\ \ln\left(\sqrt{a^2+x^2}+xight)=-\ln\left(\sqrt{a^2+x^2}-xight) \\ \ln\left(\sqrt{a^2+x^2}+xight)+\ln\left(\sqrt{a^2+x^2}-xight)=0 \\ \ln\left[\left(\sqrt{a^2+x^2}+xight)\left(\sqrt{a^2+x^2}-xight)ight]=0 \\ \left(\sqrt{a^2+x^2}+xight)\left(\sqrt{a^2+x^2}-xight)=1 \\ (a^2+x^2)-x^2=1; \ a^2=1; \ a=\pm1Максимальное значение, при котором функция нечетна, достигается при a=1Во вложениях продублировано решение для пользователей мобильного приложения и дан график функции при a=1.
    answer img

    • Автор:

      zain
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years