-
задание на вступительных в 10 класс, решите уравнение
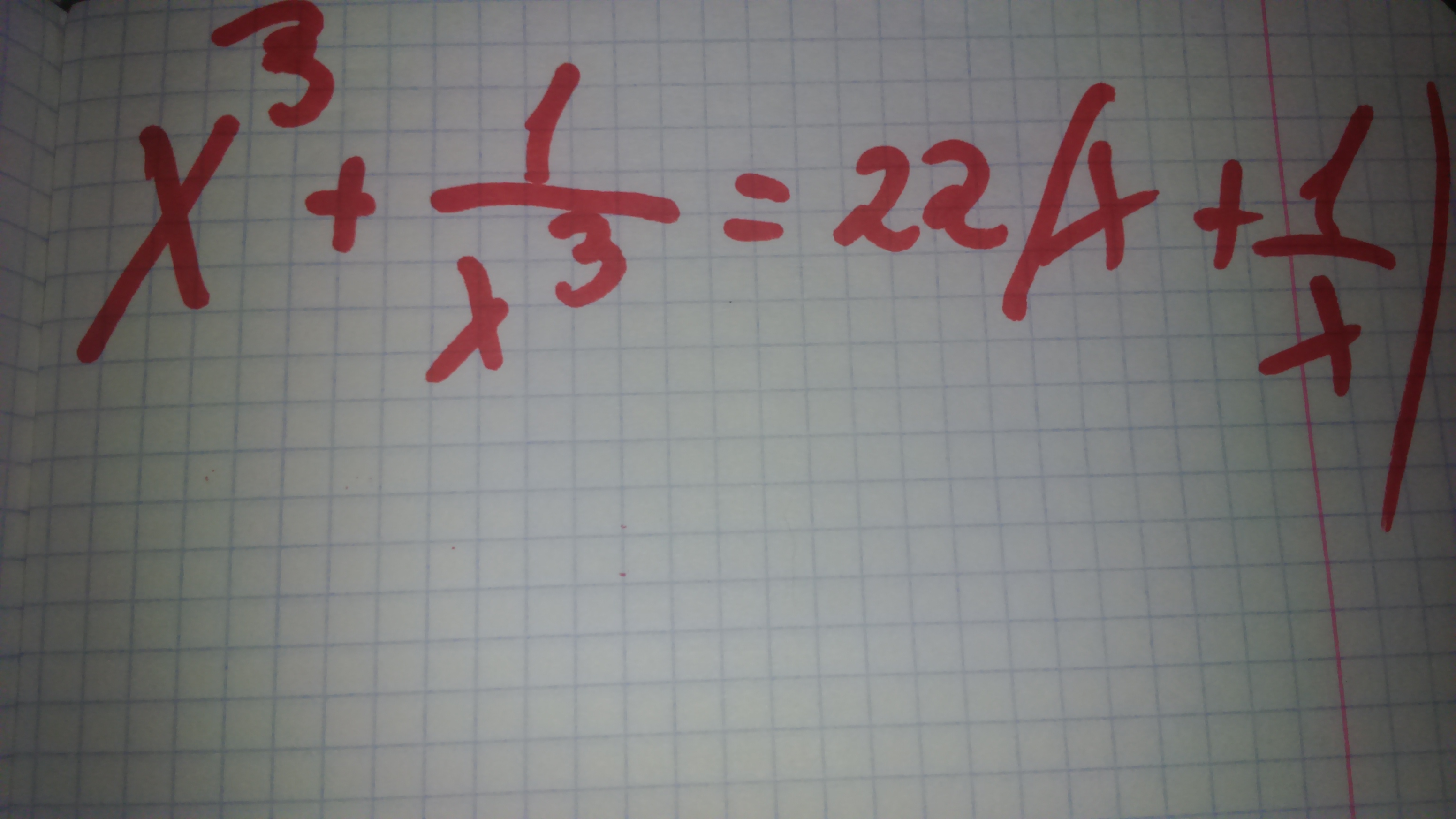
-
Предмет:
Математика -
Автор:
reese52 - 6 лет назад
-
Ответы 1
-
Для начала найдем как выразить x³+1/x³ через x+1/x.(x+1/x)³=x³+3x²*1/x+3x*1/x²+1/x³=x³+3x+3/x+1/x³=x³+1/x³+3(x+1/x). Отсюда:x³+1/x³=(x+1/x)³-3(x+1/x)Значит уравнение можно переписать так:(x+1/x)³-3(x+1/x)=22(x+1/x)(x+1/x)³=25(x+1/x)Сразу делим уравнение на x+1/x (имеем право, так как x+1/x≠0):(x+1/x)²=25[x+1/x=5[x+1/x=-5[x²-5x+1=0[x²+5x+1=0Решаем обычные квадратные уравнения и получаем корни:x=(5-√21)/2x=(5+√21)/2x=-(5+√21)/2x=(√21-5)/2
-
Автор:
gaelpu5z - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- главные герои мальчик невидимка
-
главный герой мальчик невидимка
-
Предмет:
Литература -
Автор:
jorge64 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Вычислите:
а) (√8+√32)√2
б) (√27-√12)√3
в) (2√5(√125-3√5)
Раскройте скобки:
а) (√3+7)(√3-7)
б)(2√2+1)(3√2-4)
-
В город из деревни Дубки в одно время прибыли два поезда пассажирский и товарный какой поезд выехал из деревни раньше если товарный ехал медленней чем пассажирский
-
Предмет:
Математика -
Автор:
darrelllocl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
