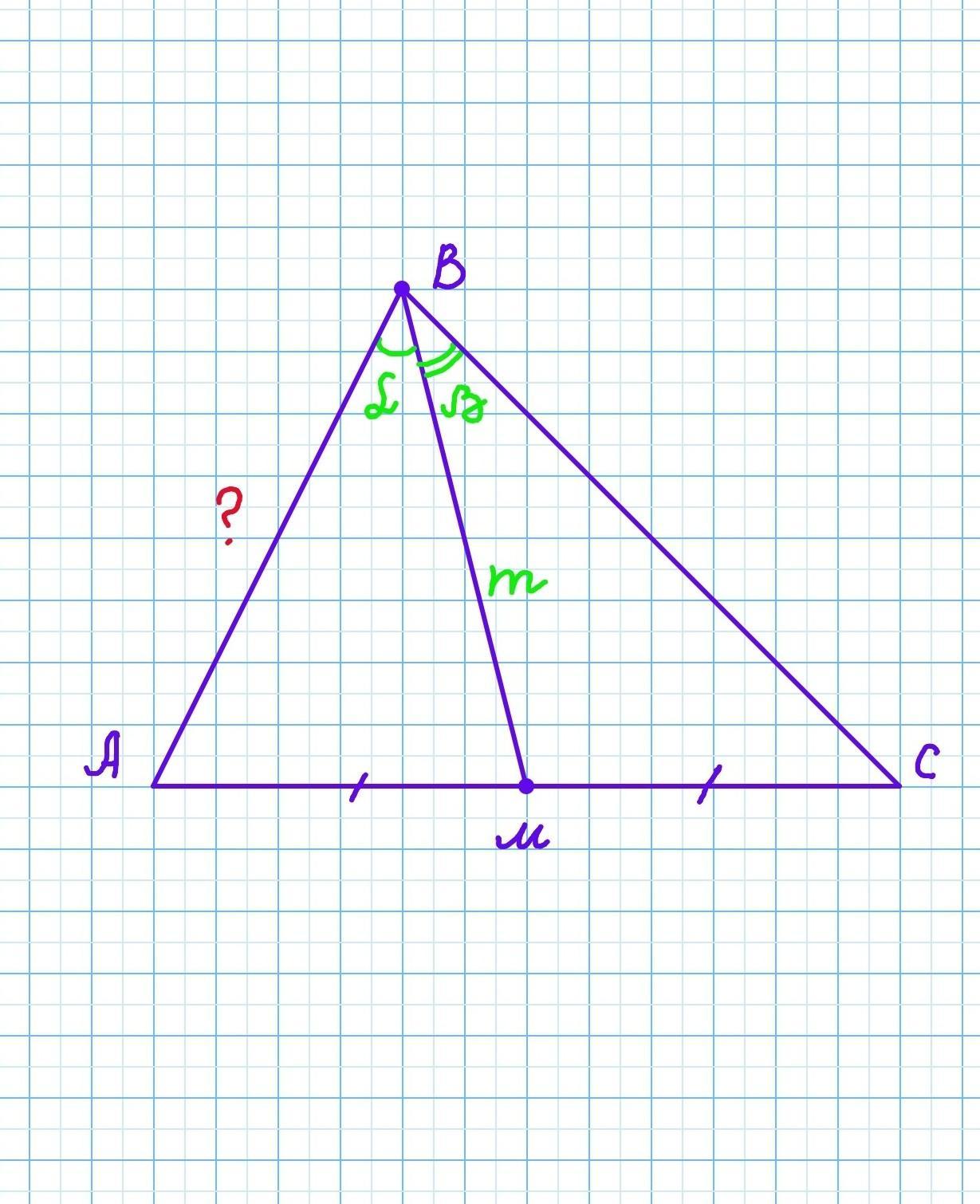
У трикутнику АВС ВМ-медіана, АВМ=альфа,МВС=бета,ВМ=m.Визначити сторону АВ

Ответ:

Сторона АВ = \dfrac{m \sin \beta }{ \sin( \alpha + \beta ) }

Пошаговое объяснение:

У трикутнику АВС ВМ-медіана, ∠АВМ= α, ∠МВС=ß, ВМ= m. Визначити сторону АВ.

1) △ABC.

ВМ медіана. Так як медіана трикутника сполучає вершину трикутника із серединою протилежної сторони, то AC=2AM=2MC.

∠ABC=∠ABM+∠MBC=α+ß.

За теоремою синусів маємо:

\dfrac{AB}{sin \angle C} = \dfrac{AC}{sin \angle B} \: \: \Rightarrow \: \: \: \dfrac{AB}{sin \angle C} = \dfrac{2MC}{sin( \alpha + \beta )}

Звідси:

(1) \boxed {sin \angle C = \dfrac{AB\cdot sin( \alpha + \beta )}{2MC} }

2) △MBC.

За теоремою синусів маємо:

\dfrac{BM}{sin \angle C} = \dfrac{MC}{sin \angle MBC} \: \: \Rightarrow \: \: \dfrac{m}{sin \angle C} = \dfrac{MC}{sin \beta}

Звідси:

(2) \boxed{sin \angle C = \dfrac{m\cdot sin \beta}{MC} }

Прирівняємо вирази (1) та (2):

\dfrac{AB\cdot sin ( \alpha + \beta )}{2MC} = \dfrac{m\cdot sin \beta }{MC}

\dfrac{AB\cdot sin ( \alpha + \beta )}{2} = m\cdot sin \beta

\bf AB = \sf \dfrac{2m\cdot sin\beta }{sin (\alpha + \beta )}

#SPJ5