Задать вопрос Регистрация
Помочь другим

  • Объясните не понимающему .Все уравнения нормально идут ,а на этом сижу.

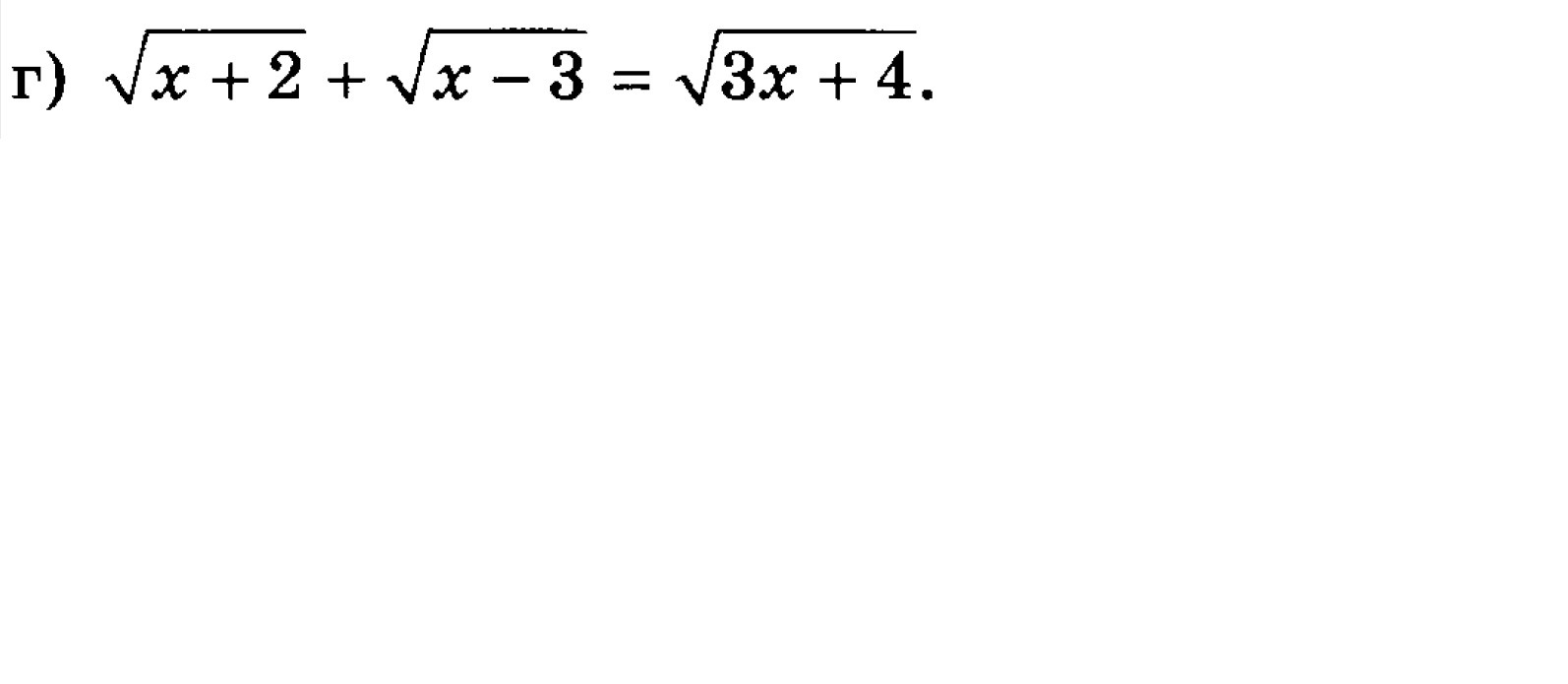
    question img

Ответы 1

  • \sqrt{x+2}+\sqrt{x-3}=\sqrt{3x+4}Подкоренное выражение неотрицательно, поэтому x+2 \geq 0, x\geq -2 \\ x-3 \geq 0, x\geq 3 \\ 3x+4\geq 0, x \geq -\frac{4}{3}Эти условия эквивалентны одному условию x \geq 3.\sqrt{x+2} + \sqrt{x-3} = \sqrt{3x+4} \\ (\sqrt{x+2} + \sqrt{x-3})^2 = 3x+4 \\ (x+2)+(x-3)+2\sqrt{(x+2)(x-3)}=3x+4 \\ 2x-1+2\sqrt{(x+2)(x-3)}=3x+4 \\ 2\sqrt{(x+2)(x-3)}=x+5 \\ 4(x+2)(x-3) = (x+5)^2 \\ 4x^2-4x-24=x^2+10x+25 \\ 3x^2-14x-49=0\\ D=14^2+4\cdot 49 \cdot 3=784=28^2 \\ x_1=\frac{14+28}{6}=7 \\ x_2=\frac{14-28}{6}=-\frac{7}{3}Второй корень квадратного уравнения не удовлетворяет условию x\geq 3, поэтому единственным решением исходного уравнения является x=7.

    • Автор:

      robin
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years