Решите пожалуйста! Что сможете! Побольше разъяснений !

Решите пожалуйста! Что сможете! Побольше разъяснений !
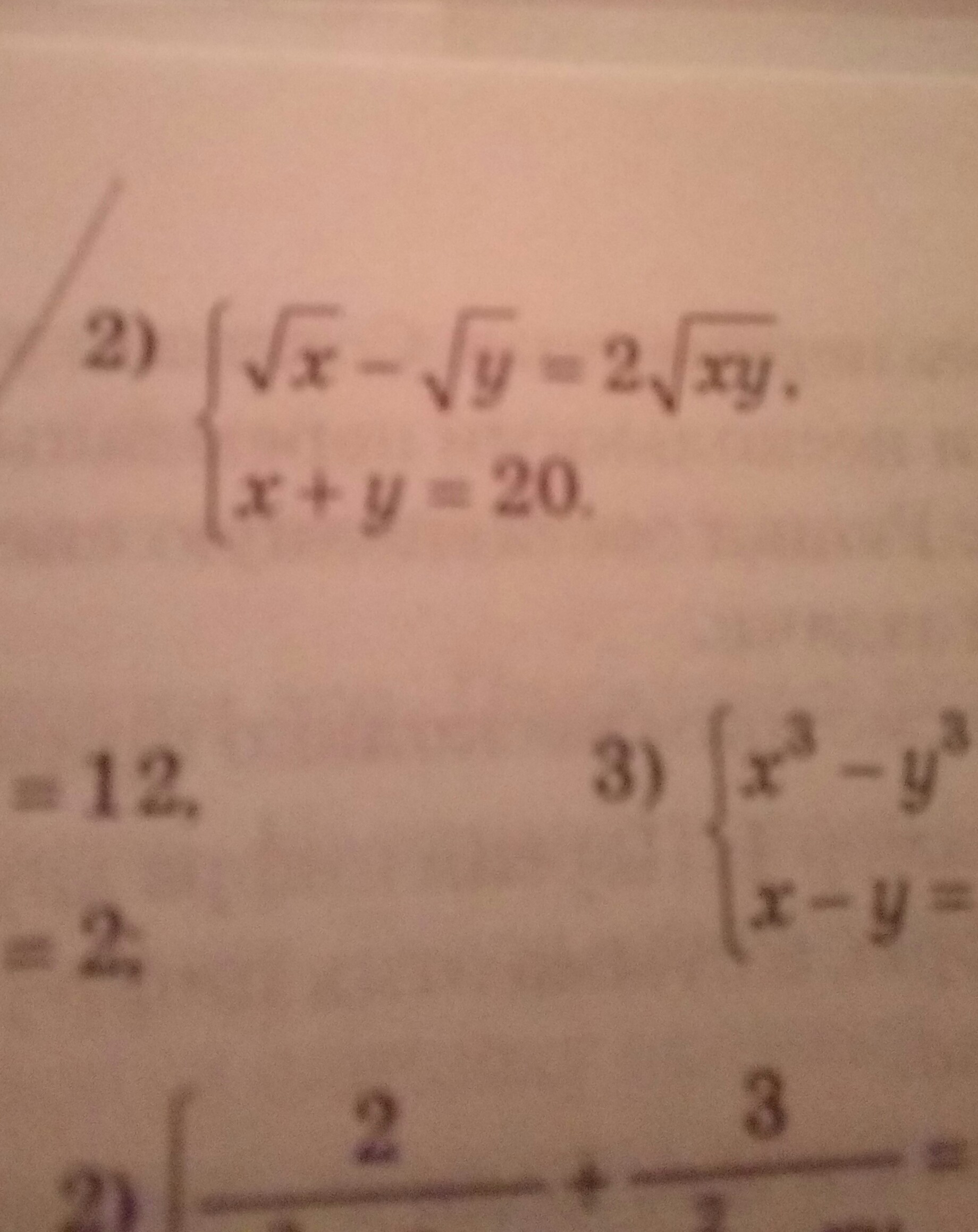
- Предмет:
  Математика
- Автор:
  pecan
- 5 лет назад

Ответы 2

черт, случайно нажал отправить ответ, ну надеюсь ты понял ход решения
- Автор:
  gallardo
- 5 лет назад
- 0
$\left \{ {{ \sqrt{x} - \sqrt{y} =2 \sqrt{xy}} \atop {x+y=20}} ight.$ выразим из второго уравнения в системе икс через игрек $\left \{ {{ \sqrt{x} - \sqrt{y} =2 \sqrt{xy} } \atop {x=20-y}} ight.$ подставим икс из второго уравнения системы в икс первого уравнения системы поучится $\sqrt{20-y} - \sqrt{y}=2 \sqrt{(20-y)y}$ раскроем скобки правой части уравнения $\sqrt{20-y} - \sqrt{y}=2 \sqrt{20y-y^{2} }$ возведем обе части уравнения в квадрат ( то есть возведем каждый член уравнения в квадрат корни после этого действия уйдут а два в квадрате будет 4) $(\sqrt{20-y}) ^{2} - ( \sqrt{y}) ^{2}= (2 \sqrt{20y- y^{2} }) ^{2}$ [/tex] $20-y-y=4(20y- y^{2})$ $20-2y=80y-4 y^{2}$ $4y^2-82y+20=0$ $a=4: b=-82: c=20$ $D= b^{2} -4ac$ $D=(-82 ^{2}) -4*4*20=6724-320=6404\ \textgreater \ 0$ $y_{1;2}=(-b+- \sqrt{D})/2a$ $y_{1;2} =(82+- \sqrt{6404})/8$ $y_{1}=(82+ \sqrt{6404})/8$ $y_{2}= (82- \sqrt{6404})/8$ итак $\left \{ {{ y_{1}=(82+ \sqrt{6404})/8 } \atop { x_{1}=20-y_1 } ight.$ $x_1=20-(82+ \sqrt{6404})/8$ возведем обе части уравнения в квадрат $x_1^{2} =400-(6724-6404)/8= 400-(320/8)=400-40= 380$ x_1= $\sqrt{380}$ ≈19,5 $x_{2}=20-(82- \sqrt{6404})/8$ $x_{2} ^2=400-((6724+6404)/8=400-13128/8=400-1641=-1241$ $x_{2}= \sqrt{-1241}=35,2$
- Автор:
  petronila
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Решите пожалуйста! Что сможете! Побольше разъяснений !

Ответы 2

Топ пользователей