-
ПОМОГИТЕ СРОЧН!
ABCD - ТРАПЕЦИЯ, AD=15 CM. НАЙТИ СЕ!!!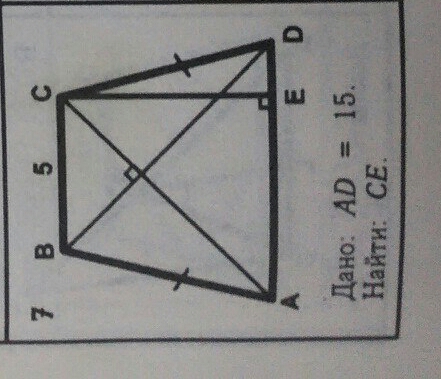
-
Предмет:
Математика -
Автор:
aureliaso0n - 6 лет назад
-
Ответы 1
-
Как видно из рисунка, данного в приложении к вопросу, трапеция равнобедренная. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, её высота равна полусумме оснований ( средней линии)- свойство. Подробно: Рассмотрим равнобедренную трапецию АВСD, АС⊥ВDПроведем через вершину С параллельно АВ прямую до пересечения с продолжением АD в точке К. Четырехугольник ВСКD - параллелограмм ( ВС║АК по условию, СК║ВD по построению). Следовательно, DК=ВС=5.В равнобедренной трапеции диагонали равны. Так как СК║ВD, ∠АСК =∠АОD как соответственный при пересечении параллельных прямых секущей. Следовательно, треугольник АСК прямоугольный равнобедренный, его высота, как высота равнобедренного треугольника, является его медианой, а острые углы равны 45°, и ∆ АС=∆ КСЕ с общим катетом СЕ. (Медиана прямоугольного треугольника равна половине гипотенузы) Значит, СЕ=АЕ=ЕК. АD+DK=15+5=20CE=20:2=10 см

-
Автор:
jennahamilton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Луч ОС биссектриса развёрнутого угла АОВ. Угол EOF прямой EOC 25. Найдите градусную меру углов АОЕ COF и FOB запишите равные углы
-
Предмет:
Математика -
Автор:
leandronewman - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Четыре необособленных предложения из рассказа Муму
-
Предмет:
Русский язык -
Автор:
buckley - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как правильно сказать .Хоть кол на голове.......
-
Предмет:
Русский язык -
Автор:
yaeldudley - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
помогите решить (a+b)/2=0,6b
-
Предмет:
Математика -
Автор:
dulce142f - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
