Задать вопрос Регистрация
Помочь другим

  • исследовать ряд на абсолютную и условную сходимость


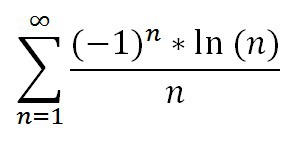
    question img

Ответы 1

  • \sum\limits _{n=1}^{\infty } \frac{(-1)^{n}ln(n)}{n} \\\\1)\quad \sum \limits _{n=1}^{\infty }\frac{ln(n)}{n}\; ;\\\\Integralnuj\; priznak:\int \limits _{1}^{+\infty }\frac{lnx}{x}dx=\lim\limits _{A\to +\infty }\int \limits _{1}^{A}\frac{lnx}{x}dx=\lim\limits _{A\to +\infty }\left (\frac{ln^2x}{2}|_1^{A}ight )=\\\\=\lim\limits _{A\to +\infty }\left (\frac{ln^2A}{2}-\frac{ln1}{2}ight )=[\, +\infty -0]=+\infty \; \; \Rightarrow \; \; rasxoditsya2)Priznak\; Lejbnica:\\\\a)\; \; \frac{ln1}{1} < \frac{ln2}{2} < \frac{\ln3}{3} >\frac{ln4}{4}>\frac{ln5}{5}>...> \frac{ln(n)}{n}>... \\\\b)\; \; \lim\limits _{n\to \infty }\frac{ln(n)}{n}= \lim\limits_{n\to \infty } \frac{1/n}{1}=0Так как ряд из абсолютных величин (модулей) расходится, то нет  абсолютной сходимости. Но выполняются условия признака Лейбница. Поэтому заданный знакочередующийся ряд сходится условно. 

    • Автор:

      turkey
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years