-
Найти площадь фигуры, ограниченной линиями.
Вычислить объем тела, полученного вращением вокруг оси 0у фигуры, ограниченной линиями, х = 0 при х> 0.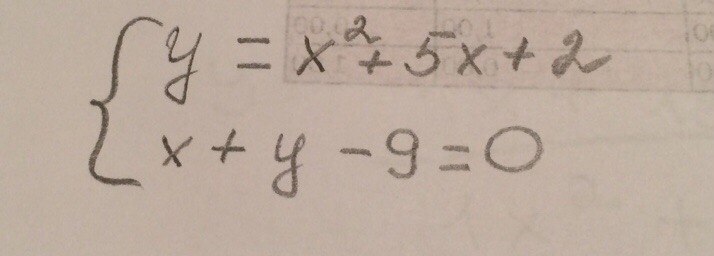
-
Предмет:
Математика -
Автор:
beetle13 - 6 лет назад
-
Ответы 3
-
Теперь объем верный. Кстати, незачем было возиться с двумя конусами, когда можно считать так же, как вы считали площадь фигуры между кривыми, как интеграл от разности верхней функции и нижней. Только в данном случае умноженной на 2pi*x. Тем более, что разность у вас уже посчитана. Т.е. вам всего-то надо было найти 2pi∫x(x²+6x-7)dx по отрезку [0,1]. Только с минусом, т.к. вы почему-то из нижней функции вычли верхнюю.
-
Автор:
pirate - 6 лет назад
-
0
-
-
Потапов можешь написать мне личное сообщение ,(хочу спросить по поводу математик и )у меня баллов нет чтобы тебе написать .
-
Автор:
picklegtgb - 6 лет назад
-
0
-
-
Задание 1 - площадь фигуры.1) Y= x²+5x+2 - парабола2) F = -x+9 - прямая.НАЙТИПлощадь фигуры.ДУМАЕМПлощадь - интеграл функции.Площадь фигуры - разность площадей.РЕШЕНИЕ.Находим пределы интегрирования - решение системы уравнений -Y(x)=F(x).3) x²+5x+2 = -x+9Упрощаем4) x²+6x-7 = 0.Решаем квадратное уравнение. Дискриминант D=64/Корни - х1 =-7 и х2 = 1 - это пределы интегрирования.YНаходим разность функций и её интеграл∫[x²+5x+2 - (-1)x -9 ]dx = ∫(x²+6x-7)dx =x³/3 + 3*x² - 7*x.Делаем подстановки пределов интегрирования - от -7 до 0.S(1) = 1/3 + 3-7 = - 3 2/3S(-7) = -114 2/3 - 147 + 49 =81 2/3 Площадь - разность - 81 2/3 - (-3 2/3) = 85 1/3 - ОТВЕТЗадание 2 - объем фигуры при Х>0 - рис. 2.Находим сумму объемов - конуса - R=1, h=1.и тела вращения - параболы Y=x²+5x+2.Формулы для расчета на рисунке (ОТВЕТ V = 2,5 *π ~ 7.85

-
Автор:
piperpatel - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите пожалуйста, срочно надо!!!
Рассчитайте массу железа, которое окислилось при ржавлении, если с трубы убрали оксид железа(3) массой 480г.-
Предмет:
Химия -
Автор:
corbinwalters - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сиим продал 3,5ц яблок и получил за это 1456 евро. Сколько получит Сиим за продажу 12 тонн яблок?
-
Предмет:
Математика -
Автор:
quinn - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Когда преступление считаете оконченным:
а) когда преступник достиг своей цели
б) когда содеянное содержит все объективные и субъективные признаки состава преступления, предусмотренного статьей Особенной части УКРФ
в) когда наступило преступное последствие
г) когда нарушено уголовно-правовая норма -
Помогите перевести на английский. Заранее спасибо
1. Как себя чувствует Джо? - Неважно, ему нездоровится.
2. Какая у него девушка? - Она привлекательная и жизнерадостная.
3. Как выглядит парень Анны? - Он худощавый брюнет высокого роста.
4. Как идёт твой бизнес? - Ужасно.
5. Как твои успехи в университете? - Пока все хорошо, но сессия уже не за горами.
6. Как выглядит его сестра? – Она похожа на Пенелопу Крус – знойная брюнетка.
7. Как твое настроение сегодня? – Лучше не бывает.
8. Как твой английский? – Делаю успехи. (improve)
9. Как его бизнес? – Дела идут в гору.
10. Какой он, твой-
Предмет:
Английский язык -
Автор:
boo53 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
