-
Найти общее решение дифференциального уравнения.
Там e^x\x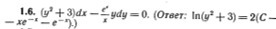
-
Предмет:
Математика -
Автор:
niapatton - 5 лет назад
-
Ответы 3
-
всё круто спасибо мне тут добрый человек помогает не в обиду если ему дам лучший ответ?
-
Автор:
adelinebaldwin - 5 лет назад
-
0
-
-
Уравнение легко приводится к виду
Правый интеграл берем по частям.u=x => du=dxdv=e^(-x)dx => v=-e^(-x)
Второй:
Таким образом:
Если не видно формулы, зайди через браузер вместо приложения.
-
Автор:
collin - 5 лет назад
-
0
-
-
(y²+3)dx=e^*ydy/xx(y²+3)dx=e^x*ydyydy/(y²+3)=xdx/e^x
u=x,dv=dx/e^x,du=dx,v=-1/e^x
-
Автор:
buffalousnd - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какой вид будут иметь символ атома хлору, если его валентные электроны обозначаются точками возле символа?
очень срочно!-
Предмет:
Химия -
Автор:
griffin323 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста, решить систему)
{1/x-1/y=1/6
{x+y=5 -
срочно !!!!!!!! главная мысль рассказа он живой и светится
-
Предмет:
Литература -
Автор:
mocha48 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Программа для PascalABC : нужен рисунок где будет дом с трубой ,небо,земля,солнце и гараж помогите плиз срочно!!!
-
Предмет:
Информатика -
Автор:
bonnieford - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
