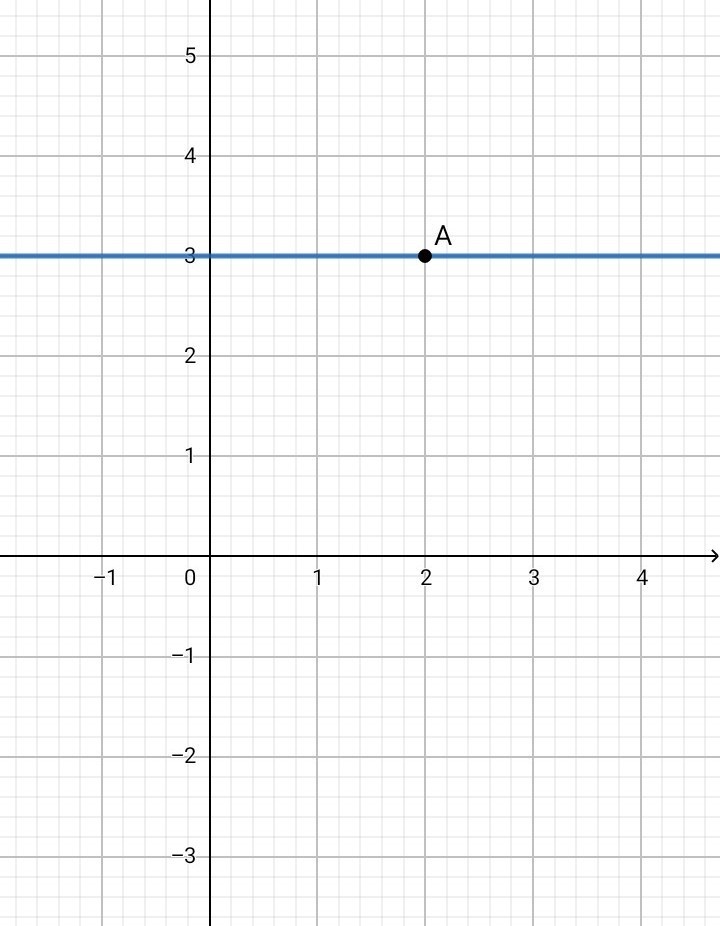
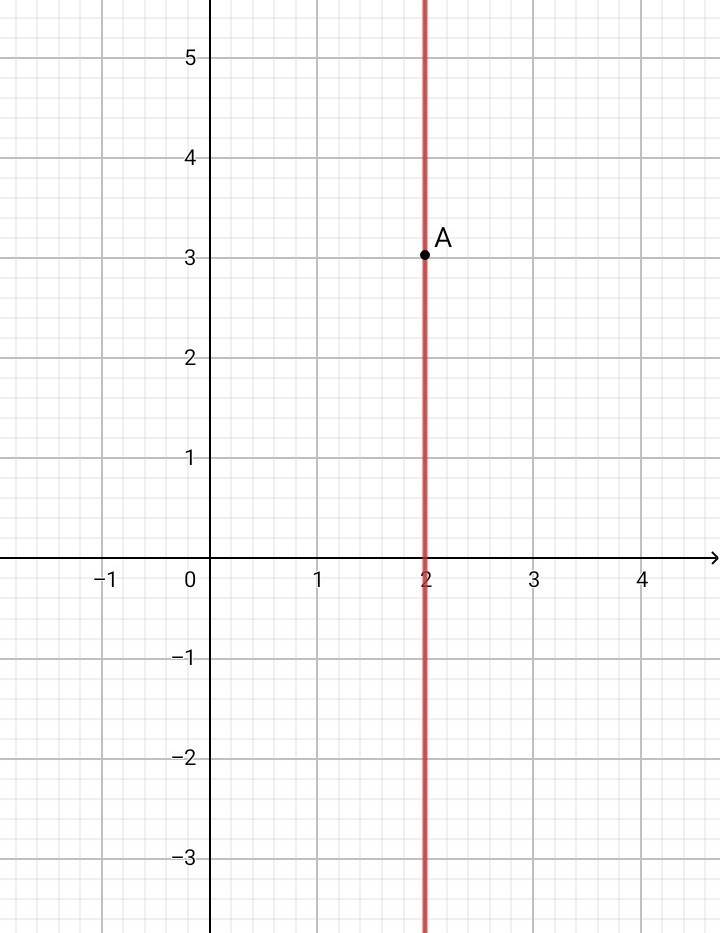
1. Составить уравнение прямой, проходящей через точку А(2;3):
a) параллельно оси Ox;
b) параллельно оси Oy.

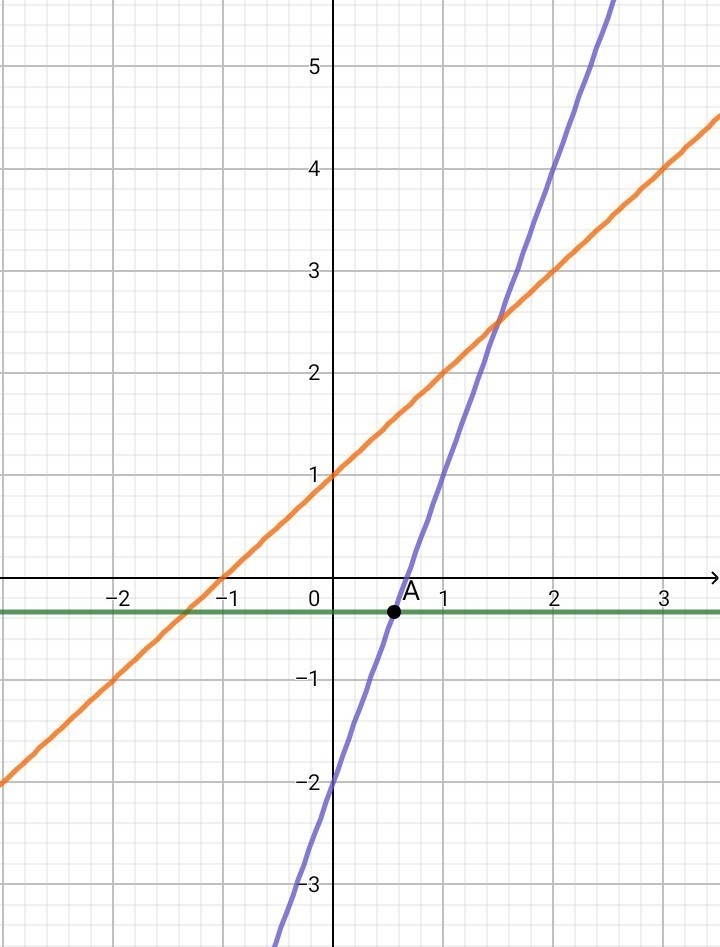
2. Составить уравнения прямых, проходящих через точку пересечения 3y+1=0 и 3x-y-2=0 параллельно и перпендикулярно прямой y=x+1.

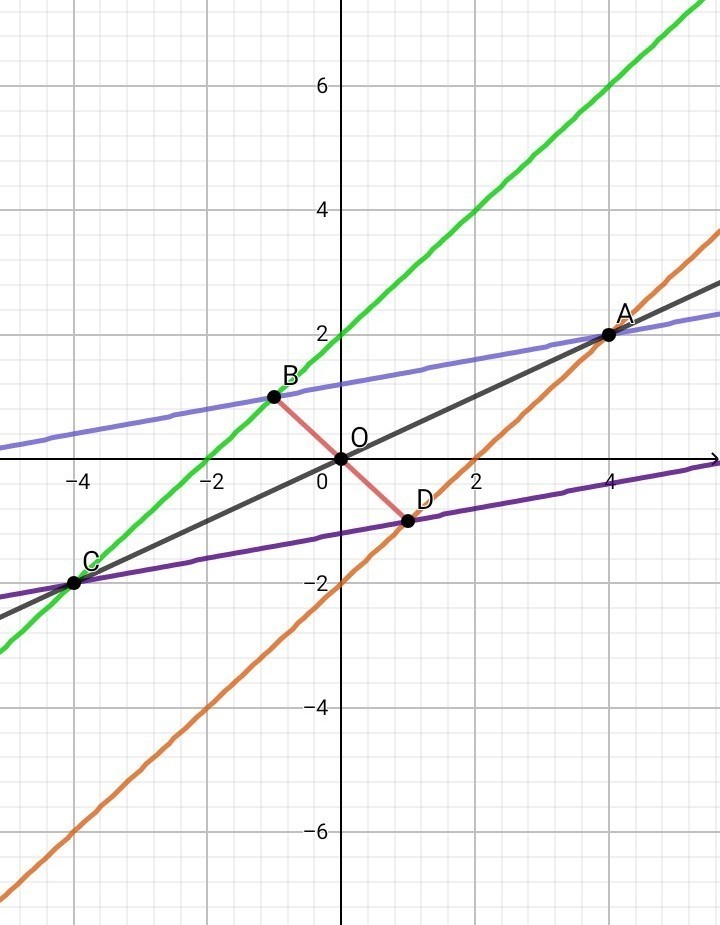
3. Две стороны параллелограмма заданы уравнениями y=x-2 и x-5y+6=0. Диагонали его пересекаются в начале координат. Найти уравнение двух других сторон параллелограмма и его диагоналей.

4. Составить уравнение прямой, проходящей через точку пересечения прямых x+y=4 и x-y=0 параллельно прямой x-4y+4=0.

p.s желательно поподробнее. фото.

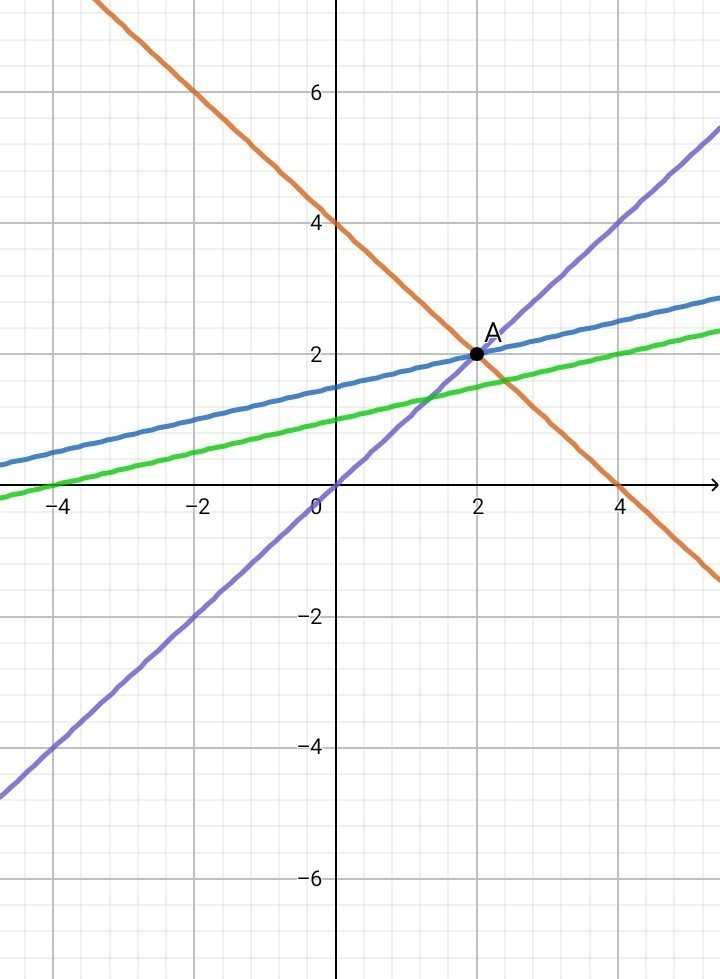
1. а) Если прямая параллельна оси Ох, то ордината ( у ) в любой точке на этой прямой одинакова и равна 3 => у = 3 ( рис. 1 )б) Если прямая параллельна оси Оу, то абцисса ( х ) в любой точке на этой прямой одинакова и равна 2 => х = 2 ( рис. 2 )2. Рисунок 3 3у + 1 = 0 => у = - 1/3 ( зел. прямая ) 3х - у - 2 = 0 => у = 3х - 2 ( фиол. прямая )Две прямые пересекаются в одной точке, координаты которой являются общими и для первой и для второй прямой. В этой точке абцисса и ордината двух прямых равны =>3х - 2 = - 1/33х = 2 - 1/33х = 5/3х = 5/9 ; у = - 1/3Значит, координаты точки пересечения двух прямых - A( 5/9 ; - 1/3 )Составим уравнение прямой, проходящей через точку А( 5/9 ; - 1/3 ) параллельно прямой y = x+1.По-первых, у = kx + b - линейная функция, где k - угловой коэффициент.Во-вторых, есть формула, по которой можно составить искомое уравнение прямой, параллельной другой прямой:у - у0 = k • ( x - x0 ) , где А( х0 ; у0 )y - ( - 1/3 ) = x - 5/9 y + 1/3 = x - 5/9y = x - 8/9 Составим уравнение прямой, проходящей через точку А( 5/9 ; - 1/3 ) перпендикулярно прямой y = x+1.у - у0 = ( - 1/k ) • ( x - x0 ) , где А( х0 ; у0 )y - ( - 1/3 ) = - ( x - 5/9 )y + 1/3 = - x + 5/9y = - x + 2/93. Рисунок 4 y = x - 2 ( оранж. прямая ) x - 5y + 6 = 0 => y = ( x + 6 ) / 5 ( син. прямая )Найдём координаты точки пересечения этих прямых:х - 2 = ( х + 6 ) / 55х - 10 = х + 64х = 16х = 4у = х - 2 = 4 - 2 = 2Значит, координаты точки пересечения двух прямых - А( 4 ; 2 )Диагональ параллелограмма проходит через точку А( 4 ; 2 ) и по условию также через начало координат О( 0 ; 0 ). Получаем уравнение прямой для первой диагонали параллелограмма АС:у = kx , A( 4 ; 2 ) k = y/x = 2/4 = 1/2 => y = x / 2Точка О( 0 ; 0 ) - точка пересечения диагоналей параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам. Отложим отрезок ОС, равный отрезку АО => получаем точку С ( - 4 ; - 2 ). Противоположные стороны параллелограмма параллельны. Составим уравнение прямой, проходящей через точку С( - 4 ; - 2 ) параллельно прямой y = ( х + 6 ) / 5у - у0 = k • ( x - x0 )y - ( - 2 ) = ( 1/5 ) • ( x - ( - 4 ) )y + 2 = ( 1/5 ) • ( x + 4 )y = ( x/5 ) + ( 4/5 ) - 2y = ( x/5 ) - ( 6/5 ) y = ( x - 6 ) / 5 ( фиол. прямая )Составим уравнение прямой, проходящей через точку C( - 4 ; - 2 ) параллельно прямой y = x - 2.у - у0 = k • ( x - x0 )у - ( - 2 ) = х - ( - 4 )у + 2 = х + 4у = х + 2 ( зел. прямая )Найдём координаты точки пересечения прямых у = ( х + 6 ) / 5 и у = х + 2:х + 2 = ( х + 6 ) / 55х + 10 = х + 6 4х = - 4х = - 1у = х + 2 = - 1 + 2 = 1Значит, координаты точки пересечения двух прямых - В( - 1 ; 1 )Диагональ параллелограмма проходит через точку В( - 1 ; 1 ) и по условию также через начало координат О( 0 ; 0 ). Получаем уравнение прямой для второй диагонали параллелограмма ВD:у = kx ; B( - 1 ; 1 )k = y/x = 1/-1 = - 1y = - x4. Рисунок 5 x + y = 4 => y = 4 - x ( оранж. прямая ) x - y = 0 => y = x ( фиол. прямая )Найдём координаты точки пересечения этих прямых:4 - x = x2x = 4x = 2y = 2Значит, координаты точки пересечения двух прямых - A( 2 ; 2 )Составим уравнение прямой, проходящей через точку А( 2 ; 2 ) параллельно прямой у = ( х + 4 ) / 4 ( зел. прямая ):у - у0 = k • ( x - x0 )у - 2 = ( 1/4 ) • ( х - 2 )у = ( х - 2 ) / 4 + 2у = ( х + 6 ) / 4 ( син. прямая )