Задать вопрос Регистрация
Помочь другим

  • СРОЧНО ПОМОГИТЕ РЕШИТЬ 6-7 ПРИМЕРОВ или больше по желанию! Даю 99 баллов за задание!!! Тема “ Вычисление производной ” Если кто может, сфотографируйте решение и выложите картинками, буду очень признателен!!!!!
    Задание: Для функций y = f (x) найти f ’(x)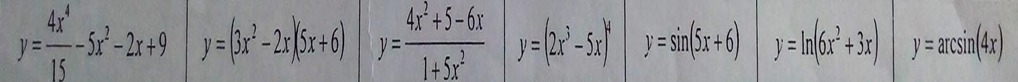

    question img

Ответы 3

  • Спасибо большое, всё просто идеально!

    • Автор:

      moose3syc
    • 5 лет назад
    • 0
  • Владей!
  • ( \frac{4}{15}x^4-5x^2-2x+9)'= \frac{4}{15}*4x^3-5*2x-2= \\ \\ 1 \frac{1}{15}x^3-10x-2 ((3x^2-2x)(5x+6))'=(3x^2-2x)'(5x+6)+(3x^2-2x)(5x+6)'= \\ (3*2x-2)(5x+6)+(3x^2-2x)*5= \\ (6x-2)(5x+6)+15x^2-10x= \\ 30x^2-10x+36x-12+15x^2-10x= \\45x^2+16x-12( \frac{4x^2+5-6x}{1+5x^2})'= \frac{(4x^2+5-6x)'(1+5x^2)-(4x^2+5-6x)(1+5x^2)'}{(1+5x^2)^2}= \\ \\ \frac{4*2x-6)(1+5x^2)-(4x^2+5-6x)(5*2x)}{1^2+2*5x^2+25x^4}= \frac{8x-6+40x^3-40x^3+50x-60x^2}{25x^4+10x^2+1}= \\ \\ \frac{60x^2-58x+6}{25x^4+10x^2+1} ((2x^3-5x)^4)'=4(2x^3-5x)^3*(6x^2-5)=(2x^3-5x)^3(24x^2-20)(sin(5x+6))'=5cos(5x+6)(ln(6x^2+3x))'= \frac{(6x^2+3)'}{6x^2+3x}= \frac{12x}{6x^2+3x} (arcsin4x)'= \frac{1}{ \sqrt{1-(4x)^2} } *(4x)'= \frac{4}{ \sqrt{1-16x^2} }

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years