Задать вопрос Регистрация
Помочь другим

  • Вычислите предел функции, не пользуясь при этом правилом Лопиталя

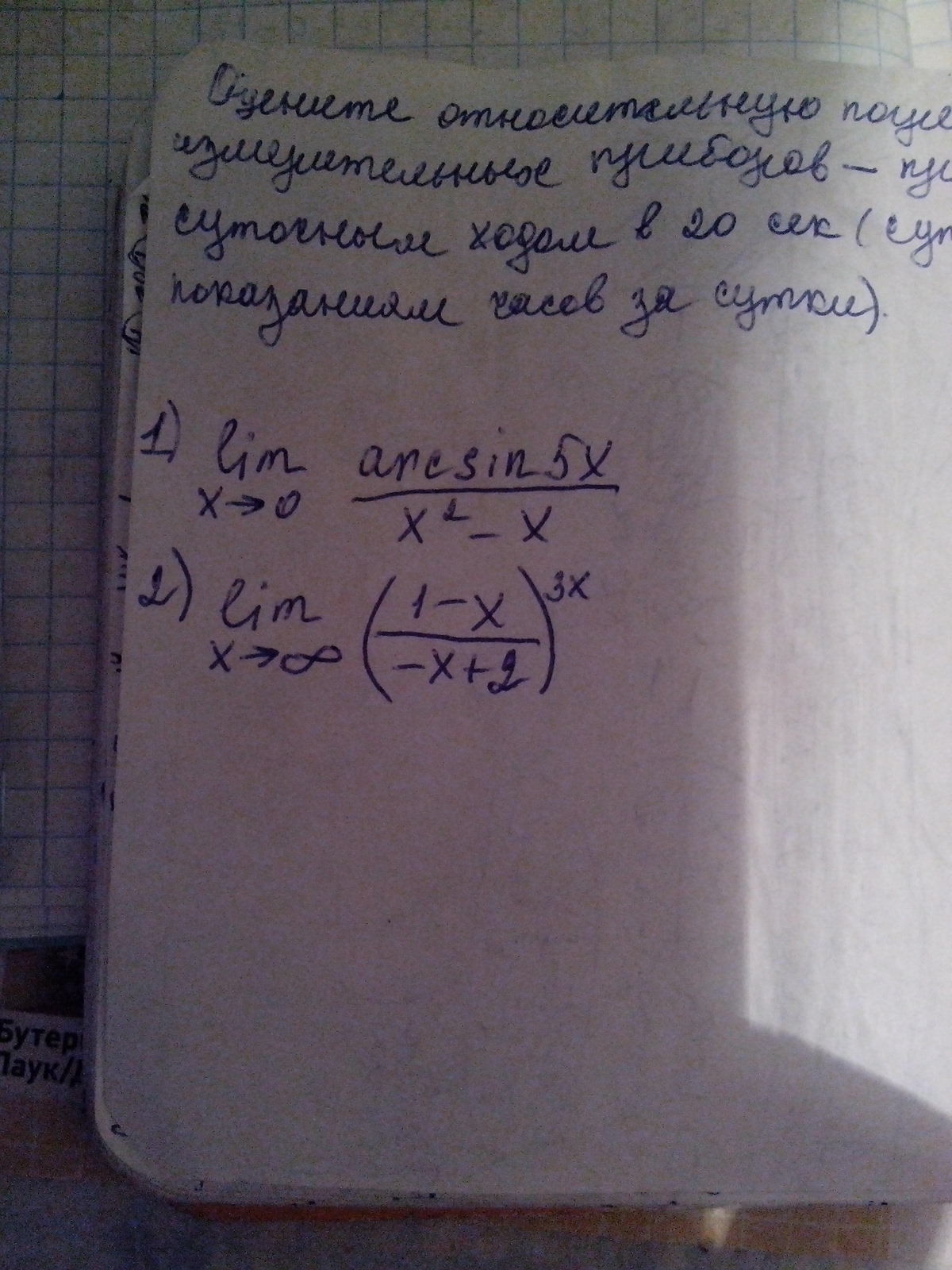
    question img

Ответы 1

  • 1.  \lim_{x \to 0} ( \frac{arcsin(5x)}{ x^{2} -x} ) Так как 5x стремится к 0 при x->0, то arcsin(5x) эквивалентен 5x. \lim_{x \to 0} \frac{5x}{x(x-1)} = \lim_{x \to 0} \frac{5}{x-1}=-52. \lim_{x \to \infty} ( \frac{1-x}{-x+2} )^{3x} = \lim_{x \to \infty} (1+ \frac{1-x +x-2}{-x+2} )^{3x}= \\ =\lim_{x \to \infty} (((1+\frac{1}{x-2} )^{x-2})^{\frac{1}{x-2}})^{3x}=\lim_{x \to \infty} e^{ \frac{3x}{x-2} }=e^3

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years