Задать вопрос Регистрация
Помочь другим

  • Срочно!!! Пожалуйста!!!
    Решить предел функции, НЕ производные, а как эквивалентно малые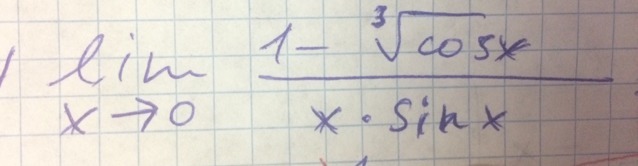

    question img

Ответы 1

  • При x->0:sin(x)~x, cos(x)=√(1-sin²(x))~√(1-x²)Тогда получим следующее: \lim_{x \to 0} \frac{1- \sqrt[3]{cos(x)} }{x*sin(x)} = \\ \lim_{x \to 0} \frac{1- \sqrt[3]{ \sqrt{1-x^2} } }{x^2} = \\ \lim_{x \to 0} \frac{1- \sqrt{ \sqrt[3]{1-x^2} } }{x^2} = \\ \lim_{x \to 0} \frac{(1- \sqrt{ \sqrt[3]{1-x^2} })(1+ \sqrt{ \sqrt[3]{1-x^2} }) }{x^2*(1+ \sqrt{ \sqrt[3]{1-x^2} })} = \\ \lim_{x \to 0} \frac{1- \sqrt[3]{1-x^2} }{2*x^2} = \\ \lim_{x \to 0} \frac{(1- \sqrt[3]{1-x^2})(1+\sqrt[3]{1-x^2}+(\sqrt[3]{1-x^2})^2) }{2*x^2*(1+\sqrt[3]{1-x^2}+(\sqrt[3]{1-x^2})^2)} =\lim_{x \to 0} \frac{1- (1-x^2) }{2*x^2*3} = \\ \lim_{x \to 0} \frac{x^2 }{6*x^2} = \frac{1}{6}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years