-
Решите неравенство. 15ое задание из второй части математики профильного уровня ЕГЭ.
Для нахождения в поисковиковиках :
1/2 * logx-2(x^2 - 10*x + 25) + log5-x(-x^2 +7*x - 10) > 3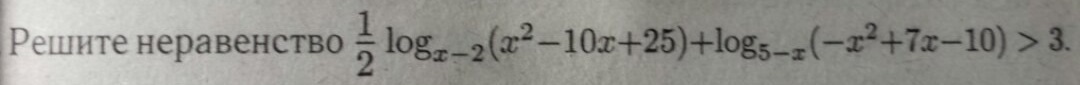
-
Предмет:
Математика -
Автор:
half pinty0qh - 6 лет назад
-
Ответы 6
-
Ваш ответ совпадает с ответом на форзаце.
-
Автор:
brenda - 6 лет назад
-
0
-
-
Просто там такой момент, что если основание логарифма от 0 до 1 то знаки неравенства нужно поменять, а если основание логарифма будет от 1 до плюс бесконечности, то знаки неравенства остаются такими, какие они есть. И оба этих момента нужно учитывать
-
Автор:
cassie40 - 6 лет назад
-
0
-
-
Это было бы важно, если бы решалось честно неравенство log(x - 2, 5 - x) > 0. Я его решаю немного по-другому. Если расписать то, что я говорю о том, что на каких-то промежутках логарифм отрицательный
-
Автор:
jabarimiddleton - 6 лет назад
-
0
-
-
то там как раз и появится разбор. А вообще для таких неравенств использовать метод рационализации, это позволит избежать рассмотрения случаев.
-
Автор:
sebastiánreese - 6 лет назад
-
0
-
-
можно ссылочку, где можно почитать этот метод рационализации?
-
Автор:
brown sugar3zj7 - 6 лет назад
-
0
-
-
Разложим квадратные трёхчлены на множители:x² - 10x + 25 = (5 - x)²-x² + 7x + 10 = (5 - x)(x - 2).Логарифмы существуют, если у них основание положительно и не равно 1, а логарифмируемое выражение положительно. В таком случае "ОДЗ" имеет вид:x - 2 > 0, x - 2 ≠ 15 - x > 0, 5 - x ≠ 1(5 - x)² > 0(5 - x)(x - 2) > 0x ∈ (2, 3) ∪ (3, 4) ∪ (4, 5).Теперь упрощаем (здесь и далее первый аргумент у логарифма - основание, второй - логарифмируемое выражение):- первое слагаемое 1/2 log(x - 2, (5 - x)^2) = log(x - 2, 5 - x)- второе слагаемое log(5 - x, (x - 2)(5 - x)) = 1 + log(5 - x, x - 2)Неравенство превращается в такое:log(x - 2, 5 - x) + 1 + log(5 - x, x - 2) > 3log(x - 2, 5 - x) + log(5 - x, x - 2) > 2Сделаем замену log(x - 2, 5 - x) = t, тогда log(5 - x, x - 2) = 1/tt + 1/t > 2Заметим, что t > 0 (t ≠ 0, так как стоит в знаменателе, а если t < 0, то левая часть отрицательна). Тогда можно домножить на t, знак не меняется:t² + 1 > 2tt² - 2t + 1 > 0(t - 1)² > 0{t > 0, t ≠ 1}Возвращаемся обратно к иксам, получаем систему{log(x - 2, 5 - x) > 0, log(x - 2, 5 - x) ≠ 1]Заметим, что если x лежит в промежутке (2, 3) или (4, 5), то первое неравенство нарушается, т.к. или основание меньше 1, а выражение больше 1, или наоборот. Поэтому из ОДЗ остаётся только (3, 4). Легко видеть, что при таких x логарифм и в самом деле положителен.Остаётся узнать, при каких x выполняется log(x - 2, 5 - x) ≠ 1. Тут никаких сложностей - нам не повезёт, только если основание и логарифмируемое выражение совпадут, т.е. когда x - 2 = 5 - x, x = 7/2. Выкалывая эту точку, получаем ответ.Ответ. x ∈ (3, 7/2) ∪ (7/2, 4).
-
Автор:
jennifermqxo - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Предприятие
а) Является собственником ресурсов
б) Не является собственником ресурсов
-
Предмет:
Экономика -
Автор:
glennbernard - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Кто такой Чубакка? (очень надо узнать, и ооочень срочно! Распростаните по возможности этот вопрос по интернету! ОЧЕНЬ НАДО ЗНАТЬ!!!)
-
Предмет:
Литература -
Автор:
alliethompson - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- шарик массой 0,1 кг совершает гармонические колебания на невесомой пружине.Определите период колебания шарика если для упругого удлинения пружины на 1 см требуется сила 0,1H
-
Из 150 кг свежих вишен получается 36 кг сушеных. Сколько процентов% сушеных вишен получается из свежих?
СРОЧНО РЕБЯТА ПОМОГИТЕ ПОЖАЛУЙСТА!!!-
Предмет:
Математика -
Автор:
cold brewifek - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
