-
Найти производные.
Прошу с ходом решения
к вопросу прилагаю фото.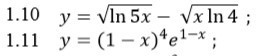
-
Предмет:
Математика -
Автор:
mccann - 6 лет назад
-
Ответы 2
-
Спасибо, я еще в 11 сократила, вытащила (1-x)³ *e^(1-x) за скобки в конце :)
-
Автор:
diego87 - 6 лет назад
-
0
-
-
1.10применим формулу производной корня ( √х)' = 1/(2√х) и учтём, что под корнем стоит сложная функция.y' = 1/(2√ln5x) * (ln5x)' - 1/(2√x*ln4) * (x*ln4)' = =1/(2√ln5x) * 1/5x * (5x)' -1/(2√x*ln4) * ln4 = = 1/(2√ln5x) * 1/5x *5 - ln4/(2√x*ln4)= 1/(2√ln5x) * 1/x - ln4/(2√x*ln4)1.11применим формулу (UV)' = U'V + UV' и учтём, что каждый множитель - сложная функция.y' = 4(1-x)³ * (1-x)' * e^(1-x) + (1-x)⁴ * e^(1-x) * (1-x)' = =- 4(1-x)³ *e^(1-x) - (1-x)⁴ * e^(1-x)
-
Автор:
krystan9q5m - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
a18, если a1=-3 , d=-2
a11, если a1=-2, d=-4-
Предмет:
Алгебра -
Автор:
carolinabarnes - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Всего-36 км. Проехал - 40 процентов. Осталось - ?
-
Предмет:
Математика -
Автор:
kianaskky - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
краткое содержание рассказа злой мальчик????
-
Предмет:
Литература -
Автор:
marley80 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Найдите стороны равнобедренного треугольника, если его периметр равен 85см, а основание в 2 раза меньше боковой стороны.
How much to ban the user?
1 hour
1 day
100 years
