-
Помогите с пределами. Заранее спасибо.
[tex] \lim_{n \to \infty} \frac{2n+3}{n+1} =2[/tex]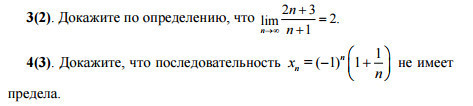
-
Предмет:
Математика -
Автор:
noé2dar - 6 лет назад
-
Ответы 4
-
Ого
-
Автор:
cubs - 6 лет назад
-
0
-
-
Я не глупый,но и то не разобрался в этих пределах
-
Автор:
petronila - 6 лет назад
-
0
-
-
Аплодисменты
-
Автор:
castaneda - 6 лет назад
-
0
-
-
1) Докажем что ∀ε>0 найдется N, такое что ∀n>N |(2n+3)/(n+1) - 2| < ε
2) По модулю все члены этой последовательности больше 1, однако при каждом следующем n знак члена последовательности меняется, поэтому при любом сколь угодно большом n будут находиться члены последовательности, модуль разности которых превышает 2, что исключает попадание всех членов последовательности в малую эпсилон-окрестность какого либо числа
-
Автор:
amazonf7od - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите пожалуйста я не как не могу решить может это легко может сложно я не понимаю
-
Предмет:
Математика -
Автор:
ticklebutt - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
помогите решить задачу на диаграмме показано распределение земель Сибири по категориям Определите По диаграмме В каких пределах находится доля земель запаса
-
Предмет:
Математика -
Автор:
groverhubbard - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сергій з батьком та матір’ю збирали гриби. Батько зібрав 46% грибів, мати – 32%, а Сергійко – решту 66 грибів. Скільки всього грибів було зібрано?
-
Предмет:
Математика -
Автор:
ivanbwwl - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
скорость велосипедиста 12км/ч , а скорость мотоциклиста 45 км/ч . сейчас расстояние между ними равно 212 км. Какое расстояние будет между ними через 3 часа?
-
Предмет:
Математика -
Автор:
giannigfsm - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
