Задать вопрос Регистрация
Помочь другим

  • Найти область сходимости степенного ряда:

    Вариант 1:
    ∞
    ∑ хⁿ÷n×3ⁿ
    ⁿ=1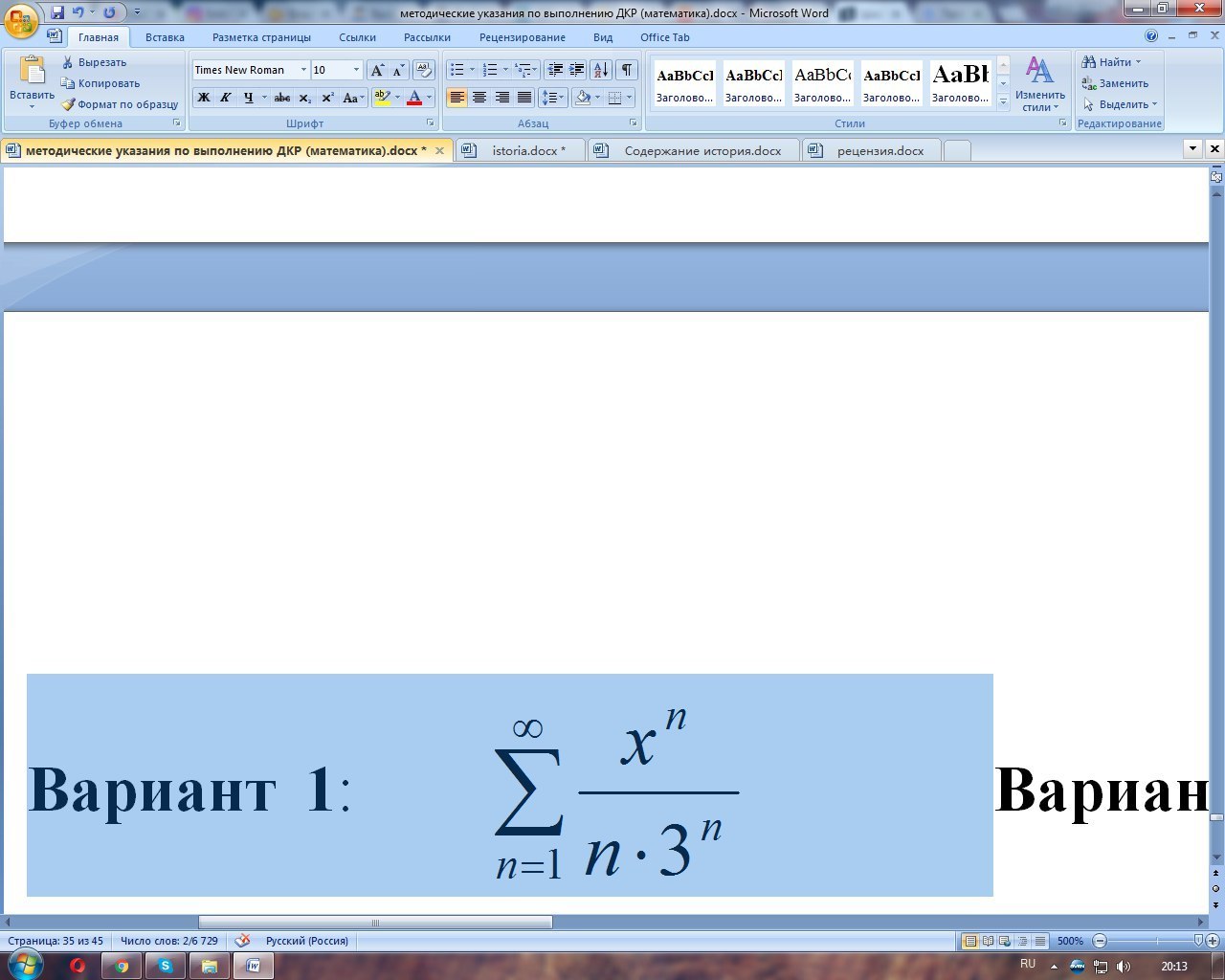

    question img

Ответы 1

  • По признаку Даламбера, если \lim_{n \to \infty} \frac{a_{n+1}}{a_n} \ \textless \ 1 То ряд сходится. \lim_{n \to \infty} ( \frac{x^{n+1}}{(n+1)*3^{n+1}}: \frac{x^n}{n*3^n} )= \lim_{n \to \infty} ( \frac{x^{n+1}}{x^n}* \frac{n}{n+1}* \frac{3^n}{3^{n+1}}) Разберем эти дроби по отдельности \lim_{n \to \infty} \frac{x^{n+1}}{x^n}* \lim_{n \to \infty}\frac{n}{n+1}* \lim_{n \to \infty}\frac{3^n}{3^{n+1}}=x*1* \frac{1}{3} = \frac{x}{3} \ \textless \ 1Очевидно, x < 3. Радиус сходимости равен 3. x ∈ [-3;3]

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years